Matematická olympiáda – kategorie P

Zadání úloh krajského kola 51. ročníku

Krajské kolo 51. ročníku MO kategorie P se koná v úterý 8.1.2002 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého času. V krajském kole MO-P se neřeší žádná praktická úloha, pro zajištění rovných podmínek řešitelů ve všech krajích je použití počítačů při soutěži zakázáno.

Řešení každého příkladu musí obsahovat:

Hodnotí se nejen správnost programu, ale také kvalita popisu řešení a efektivita zvoleného algoritmu.

Vzorová řešení úloh naleznete krátce po soutěži na Internetu na adrese http://mo.mff.cuni.cz/. Na stejném místě budou zveřejněny i výsledky všech krajských kol a seznam postupujících do celostátního kola. Naleznete zde také aktuální informace o celostátním kole kategorie P Matematické olympiády, zejména o novém prostředí, v němž budete na celostátním kole řešit praktické úlohy.

P-II-1 Matice

Uvažujme matici A o rozměrech m x n, která obsahuje pouze nuly a jedničky. Orámovaným obdélníkem budeme nazývat takovou podmatici, která má aspoň dva řádky, aspoň dva sloupce a jejíž první a poslední řádek, stejně jako první a poslední sloupec, obsahují samé jedničky. Uvnitř obdélníka mohou být libovolné prvky.

Soutěžní úloha

Navrhněte algoritmus, který v dané matici A najde největší orámovaný obdélník. Velikost orámovaného obdélníka s i řádky a j sloupci je rovna i*j (tzn. hledáme orámovaný obdélník, pro který bude součin i*j největší možný). Pokud existuje více takových obdélníků, stačí nalézt jeden libovolný z nich. Můžete předpokládat, že aspoň jeden orámovaný obdélník se v matici A nachází.

Příklad

Vstup:
m = 11, n = 24
000000000000000000000000 
001111100000000001100000 
001100111111111111111110 
001011111111111111111110 
001010100000100011100000 
001111100100100011100000 
000010001100100111111000 
000010000000100100101000 
010011111111100100001000 
001000000000000111111000 
000000000000000000000000
Výstup:
Největší orámovaný obdélník má rozměry 6 x 9 a jeho levý horní roh je ve 4. řádku a 5. sloupci.

P-II-2 Robot

Výzkumný ústav potrubí a rour má nový problém, tentokrát se soustavou orientovaných trubek. Pro vyčištění této soustavy je zapotřebí, aby čisticí robot prošel každou trubkou právě jednou. Soustava je orientovaná, což znamená, že pro každou trubku je předepsán směr, kterým musí robot trubkou projít. S vynaložením velkého úsilí se programátorům výzkumného ústavu podařilo napsat program, který pro danou soustavu trubek najde jednu možnou trasu čisticího robota, nebo zjistí, že taková trasa neexistuje. Někdy je ovšem užitečné vědět, zda existuje více různých tras čištění (střídáním čisticích tras je totiž možné snížit opotřebení robota v zatáčkách).

Soustava potrubí je složena z n uzlů očíslovaných 1,...,n, mezi nimiž vede m jednosměrných trubek očíslovaných 1,...,m. Každá trubka vede mezi dvojicí navzájem různých uzlů a nemá žádné odbočky nebo větvení. Z každého uzlu vede do každého jiného uzlu nejvýše jedna trubka. Pro tuto soustavu je zaručeno, že existuje trasa robota, která začíná i končí v uzlu 1 a projde každou trubkou právě jednou (v souladu se stanovenou orientací trubky). Pracovníci výzkumného ústavu navíc pomocí svého programu jednu takovouto trasu našli a tato trasa je vám k dispozici. Vaším úkolem je zjistit, zda existuje ještě jiná trasa začínající i končící ve vrcholu 1, která projde každou trubkou právě jednou. Tuto trasu nemusíte vypisovat, stačí, když váš program odpoví ano/ne.

Příklad

Vstup:
n = 5, m = 7
Trubky:
1 2
1 5
2 3
3 1
3 4
4 1
5 3
Trasa: 1 2 3 4 1 5 3 1
Výstup:
Existuje jiná trasa.
Poznámka:1 2 3 1 5 3 4 1 je příklad jiné trasy.
Vstup:
n = 5, m = 6
Trubky:
1 2
2 3
3 1
3 4
4 5
5 3
Trasa: 1 2 3 4 5 3 1
Výstup:
Neexistuje jiná trasa.

P-II-3 Učitel

Ve třídě sedí učitel a dává pozor na n žáků, kteří píšou písemku. Učitel se po většinu času dívá jedním směrem. Tento směr budeme nazývat základní směr. Jakmile však učitel zaslechne odněkud podezřelé zvuky, rychle se otočí, aby viděl, co se děje. Úkolem je zvolit základní směr tak, aby úhel, o který se musí otočit, byl co nejmenší. Jelikož k různým žákům je třeba natočení o různý úhel, chceme minimalizovat průměrný úhel.

Soutěžní úloha

Na vstupu je dáno číslo n a souřadnice n bodů v rovině [x1,y1], [x2,y2], ..., [xn,yn]. Každý bod určuje polohu jednoho žáka ve třídě. Učitel sedí v bodě [0,0]. Můžete předpokládat, že bod [0,0] neleží na žádné přímce určené dvěma zadanými body.

V základním směru je učitel otočen směrem k nějakému bodu [x,y]. Když zaslechne vyrušovat žáka i, otočí se směrem k bodu [xi,yi]. Otáčí se buď po směru hodinových ručiček, nebo proti směru hodinových ručiček, podle toho, kterým směrem je úhel otočení menší (tzn. pro každého žáka je úhel otočení nejvýše 180o).

Průměrný úhel otočení je aritmetický průměr úhlů otočení pro všech n bodů. Úkolem je zvolit takový bod [x,y] určující základní směr, aby průměrný úhel otočení byl nejmenší možný.

Pomůcka: Můžete předpokládat, že máte k dispozici funkci uhel(x,y), která vrátí úhel otočení učitele mezi bodem [1,0] a bodem [x,y] měřeno proti směru pohybu hodinových ručiček (tj. úhel mezi 0o a 360o).

Příklad

Vstup:
n=4, body: [-1,1], [0,-3], [-2,-2], [2,0]
Výstup:
Základní směr je směrem k bodu [-1,-2].
Poznámka: Průměrný úhel otočení je 67.5o.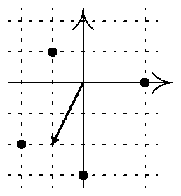

Správných řešení existuje více, například také bod [-2,-2] (žák 3).

Situace z příkladu k úloze P-II-3

P-II-4 Komparátorové sítě

Komparátorové sítě se využívají při návrhu paralelních algoritmů. Mohou se také snadno realizovat pomocí elektronických obvodů. Komparátor je jednoduché zařízení, které obdrží na vstupu dvě čísla, porovná je, na vrchním ze svých výstupů vrátí menší z těchto dvou čísel a na spodním větší z nich. Z komparátorů lze sestavovat složitější obvody, kterým budeme říkat komparátorové sítě.

Komparátorová síť je tvořena n vodorovně uspořádanými vodiči, které jsou na několika místech propojeny pomocí komparátorů. Komparátory jsou uspořádány do vrstev, které odpovídají jednotlivým krokům výpočtu. Na začátku výpočtu (v kroku 0) síť dostane na vstupu n čísel. Po skončení kroku k-1 se výstupy z kroku k-1 přenesou vodiči na komparátory ve vrstvě k. Komparátor ve vrstvě k spojuje vždy dva vodiče (nemusí to ovšem být sousední vodiče). Jestliže je na spodním z nich menší hodnota než na vrchním, vymění tyto hodnoty, v opačném případě je nechá beze změny. V jedné vrstvě může být umístěno i více komparátorů (jejich výpočet probíhá najednou, paralelně), ale v jedné vrstvě může jeden vodič vstupovat nejvýše do jednoho komparátoru. Po skončení celého výpočtu jsou na výstupech sítě tatáž čísla jako na jejích vstupech, pouze může být zaměněno jejich pořadí.

Graficky se vodiče zobrazují jako vodorovné čáry, komparátory jako svislé spojnice svých vstupních vodičů. Komparátory umístěné v jedné vrstvě se kreslí svisle nad sebe, případně do několika sousedních sloupců. Jednotlivé vrstvy sítě oddělujeme svislou čárkovanou čarou. Výpočet komparátorové sítě probíhá zleva doprava.

Při návrhu sítí se snažíme sestrojit je tak, aby doba výpočtu byla co nejmenší, tj. aby síť měla co nejméně vrstev. Druhým kritériem hodnocení kvality sítě je počet použitých komparátorů (na tomto počtu může záviset například výrobní cena sítě).

Příklad 1

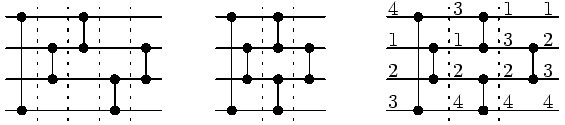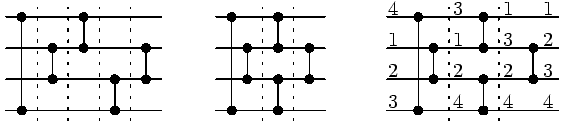
Komparátorové sítě pro 4 vstupy
Uvažujme nejlevější síť na obrázku. Tato síť dostane čtyři vstupy a vrátí je uspořádané od nejmenšího k největšímu. Po prvních dvou krocích výpočtu bude nejmenší vstup buď na prvním nebo na druhém vodiči a největší vstup na třetím nebo na čtvrtém. Další dva kroky umístí nejmenší a největší hodnotu na své místo a v posledním kroku se správně uspořádají hodnoty na druhém a třetím vodiči. Všimněte si, že první a druhý komparátor (stejně jako třetí a čtvrtý) je možné sloučit do jedné vrstvy, aniž by se tím změnil výsledek výpočtu. Výsledná rychlejší síť je na prostředním obrázku. Pravý obrázek ukazuje průběh výpočtu pro vstup 4,1,2,3.

Příklad 2

Sestrojte komparátorovou síť, která na vstupu obdrží n čísel a na výstupu umístí nejmenší z těchto čísel na první vodič. Na pořadí ostatních čísel nezáleží. Můžete předpokládat, že n je mocnina dvou.

Řešení

Síť sestrojíme rekurzívně. Označme Sn síť, která úlohu řeší pro n vstupů. Jestliže n=1, Sn nebude obsahovat žádný komparátor, neboť máme jen jediný vstup. Předpokládejme tedy, že n>1. Vstupy rozdělíme na dvě poloviny - horní a dolní. Na každou polovinu vstupů aplikujeme síť Sn/2. Tyto dvě sítě poloviční velikosti mohou pracovat paralelně. Po skončení jejich výpočtu budeme mít na vodiči číslo 1 nejmenší hodnotu z horní poloviny vstupů a na vodiči číslo n/2+1 nejmenší hodnotu z dolní poloviny. Nyní proto stačí přidat jeden komparátor mezi vodiče 1 a n/2+1 a dostaneme celkové minimum na prvním vodiči. Síť Sn se tedy skládá ze dvou sítí Sn/2 a z jednoho dalšího komparátoru. Konstrukce sítě Sn je znázorněna na následujícím obrázku vlevo, vpravo je příklad výsledné sítě pro n=8.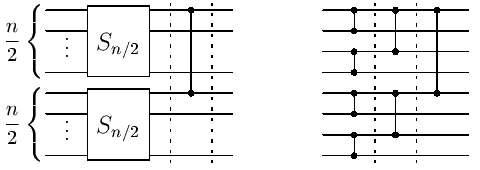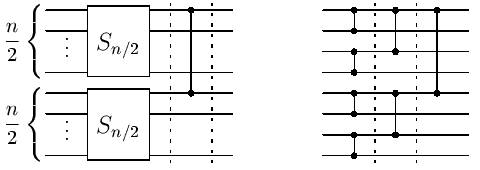

Rekurzivní výstavba sítě
Všimněte si, že hloubka rekurze je log2n, neboť velikost vstupu se v každém rekurzívním kroku sníží na polovinu. Každá úroveň rekurze přidá do výsledné sítě jednu vrstvu, takže síť Sn má log2n vrstev. Počet použitých komparátorů je v poslední vrstvě 1, v každé další vrstvě odzadu se vždy zdvojnásobí. Nechť počet vstupů je n=2k. Potom počet použitých komparátorů je 1+2+4+...+2k-1=2k-1=n-1 (součet geometrické posloupnosti). Získali jsme tedy síť, která má O(log n) vrstev a používá O(n) komparátorů.

Soutěžní úlohy

  1. Na následujícím obrázku je nakreslena komparátorová síť se šesti vstupy. Nalezněte vstupní data (tj. šestici čísel), která tato síť nesetřídí (neuspořádá je podle velikosti). Zobrazte také průběh výpočtu sítě pro tato vstupní data.

    Komparátorová síť z úlohy P-II-4 a)

  2. V komparátorové síti uvedené v části a) se nachází komparátor, po jehož odstranění bude síť správně třídit libovolnou vstupní posloupnost šesti čísel. Určete tento komparátor a vysvětlete, proč po jeho odstranění síť správně třídí.,
  3. Na vstupu komparátorové sítě je 2n navzájem různých čísel. Čísla na prvních n vstupech jsou seřazena od nejmenšího po největší a čísla na druhých n vstupech jsou také seřazena od nejmenšího po největší. Navrhněte komparátorovou síť, která na prvních n výstupech vrátí n nejmenších čísel (v libovolném pořadí) a na druhých n výstupech vrátí n největších čísel (v libovolném pořadí). Snažte se, aby vaše síť byla co nejrychlejší.

    Příklad

    Nechť n=3 a vstupy jsou 1,4,5,2,3,6. Na výstupu první tři vodiče obsahují čísla 1,2,3 v libovolném pořadí a druhé tři vodiče obsahují čísla 4,5,6 v libovolném pořadí. Například 2,3,1,6,5,4 je správný výstup.