Matematická olympiáda – kategorie P
Řešení úloh školního kola 51. ročníku
Tento pracovní materiál není určen přímo studentům - řešitelům olympiády. Má pomoci učitelům na školách při přípravě konzultací a pracovních seminářů pro řešitele soutěže, pracovníkům regionálních výborů MO slouží jako podklad pro opravování úloh domácího kola MO kategorie P. Studentům lze tyto komentáře poskytnout až po termínu stanoveném pro odevzdání řešení úloh domácího kola MO - P jako informaci, jak bylo možné úlohy správně řešit, a pro jejich odbornou přípravu na účast ve druhém kole soutěže.
P-I-1
Úlohu nejprve převedeme do terminologie teorie grafů. Bipartitní graf
je takový graf, ve kterém můžeme vrcholy
rozdělit do dvou disjunktních množin R a S tak, aby každá
hrana grafu spojovala některý vrchol z množiny R s některým
vrcholem z množiny S. Čtvercovou matici A nul a jedniček
rozměrů n x n můžeme chápat jako reprezentaci bipartitního
grafu G s 2n vrcholy, kde vrcholy r1,r2,... rn
odpovídají řádkům a vrcholy s1,s2,...,sn sloupcům matice.
Vrcholy ri a sj jsou spojeny hranou právě tehdy, když prvek
A[i,j]=1. Hranu mezi ri a sj budeme značit (ri,sj).
Řekneme, že bipartitní graf má perfektní párování, jestliže se jeho vrcholy dají uspořádat do dvojic tak, že v každé dvojici je jeden vrchol z množiny R a jeden vrchol z množiny S a tyto dva vrcholy jsou spojeny hranou. Každý vrchol grafu se přitom musí nacházet právě v jedné takovéto dvojici.
Ukážeme, že jestliže bipartitní graf G má perfektní párování, potom v naší matici A lze přerovnat řádky a sloupce takovým způsobem, aby na hlavní diagonále byly samé jedničky. Pokud párování obsahuje dvojice (ri1,sj1), (ri2,sj2), ..., (rin,sjn), pak stačí řádky uspořádat v pořadí i1, i2, ..., in a sloupce v pořadí j1, j2, ..., jn. Označme takto přerovnanou matici A'. Platí A'[k,k]=A[ik,jk]. Jelikož mezi vrcholy rik a sjk v grafu G vede hrana, platí A[ik,jk]=1, a proto matice A' má na hlavní diagonále samé jedničky.
Naopak, pokud lze matici A přerovnat tak, aby měla na hlavní
diagonále samé jedničky, pak v grafu G existuje perfektní
párování. Nechť v přerovnané matici A' jsou řádky v pořadí
i1, i2, ..., in a sloupce v pořadí j1, j2, ...,
jn. Víme, že pro všechna k platí A'[k,k]=1, a proto také
A[ik,jk]=1. Proto v grafu G dvojice (ri1,sj1),
(ri2,sj2), ..., (rin,sjn) tvoří perfektní
párování. Dokázali jsme tedy následující tvrzení:
Matici A je možné transformovat na tvar se samými jedničkami na
hlavní diagonále právě tehdy, když existuje perfektní párování
v grafu G.
Jestliže tedy chceme zjistit, jak zadanou matici A přetransformovat na tvar se samými jedničkami na hlavní diagonále, nalezneme nejprve perfektní párování v bipartitním grafu G. Pokud perfektní párování existuje, přerovnáme řádky a sloupce matice podle postupu uvedeného výše. Pokud takové párování neexistuje, matici nelze transformovat do požadovaného tvaru. Jediným problémem v tuto chvíli zůstává, jak nalézt perfektní párování bipartitního grafu.
Připomeňme si, že v perfektním párování jsou v každé dvojici vrcholy spojeny hranou. Proto můžeme perfektní párování chápat také jako množinu hran M takovou, že každý vrchol grafu je koncovým vrcholem právě jedné hrany z M. Podobně můžeme definovat párování jako množinu hran M takovou, že každý vrchol grafu je koncovým vrcholem nejvýše jedné hrany z M. To znamená, že v párování, které není perfektní, nemusí být každý vrchol zařazen do některé dvojice. Ukážeme si nyní algoritmus, jak nalézt v bipartitním grafu maximální párování, tj. párování s nejvyšším možným počtem hran.
Maximální párování budeme hledat postupně. Začneme s prázdným párováním M=0 a v každém kroku zvýšíme počet párovacích hran o jedna. Když se nám v některém kroku nepodaří zvýšit počet hran v párování, prohlásíme aktuální nalezené párování za maximální a výpočet ukončíme.
Počet hran v párování budeme zvyšovat pomocí takzvaných zlepšujících cest. Uvažujme libovolné pevně zvolené párování M. Alternující cesta pro párování M je posloupnost vrcholů ri1,sj1,ri2,sj2,...,rik,sjk, která začíná řádkovým vrcholem, končí sloupcovým vrcholem, každá dvojice po sobě jdoucích vrcholů je spojena hranou a střídají se párovací a nepárovací hrany, přičemž první hrana (ri1,sj1) je nepárovací. Zlepšující cesta je alternující cesta, která začíná i končí nespárovaným vrcholem.
Všimněte si, že zlepšující cesta P = ri1,sj1,ri2,sj2,...,rik,sjk se skládá z k-1 párovacích a k nepárovacích hran. Mějme tedy párování M a zlepšující cestu P. Jestliže všechny párovací hrany v P změníme na nepárovací a naopak, dostaneme nové párování M', které má o jednu hranu více (uvědomte si, že M' skutečně splňuje podmínky párování).

Plné čáry jsou párovací, čárkované jsou nepárovací
Dokážeme nyní, že naším postupem vždy dostaneme maximální
párování, tzn. že vždy existuje zlepšující cesta pro párování,
které není maximální.
Tvrzení
Jestliže párování M není maximální, existuje pro něj zlepšující cesta v G.Důkaz tvrzení
Nechť M je párování, které není maximální. Jelikož M není maximální, musí existovat nějaké párování M', které obsahuje více hran než M. Hrany patřící do M, ale nepatřící do M', nazveme modré, zatímco hrany patřící do M' a ne do M nazveme červené. Protože |M'|>|M|, červených hran je více než modrých.Uvažujme graf G' tvořený všemi modrými a červenými hranami. Každý vrchol v G' sousedí s nejvýše jednou modrou a jednou červenou hranou. Každá komponenta souvislosti grafu G' proto musí být buď kružnice nebo cesta, přičemž na každé kružnici i cestě se střídají červené a modré hrany. To znamená, že každá kružnice obsahuje stejný počet modrých a červených hran, počty červených a modrých hran na každé cestě se liší nejvýše o 1. Protože červených hran je více než modrých, musí existovat komponenta P, která obsahuje více červených hran než modrých. Tato komponenta musí být cestou, která začíná i končí červenou hranou. Cesta P tedy obsahuje lichý počet hran. Z toho vyplývá, že jeden z jejích konců musí být řádkovým vrcholem (nazveme ho ri) a druhý sloupcovým vrcholem (nazveme ho sj). Jelikož ri resp. sj je nespárovaný řádkový resp. sloupcový vrchol a každá druhá hrana patří do párování M, musí být P zlepšující cesta pro M.
Implementace algoritmu.
Graf G reprezentujeme samotnou maticí, tj. dvojrozměrným polem A. Pro každý vrchol ri (sj) si budeme v poli par_r (par_s) pamatovat, zda je spárovaný s nějakým vrcholem a pokud ano, číslo tohoto vrcholu. Začneme se všemi vrcholy nespárovanými. Funkce Zlepsi hledá zlepšující cestu a když ji najde, použije ji na zlepšení stávajícího párování. Hledání zlepšující cesty budeme realizovat prohledáváním do šířky ze všech vrcholů ri, které ještě nejsou spárované. Jakmile najdeme nějakou alternující cestu do nespárovaného vrcholu sj, prohledávání ukončíme. V tomto okamžiku je třeba projít po nalezené cestě z sj zpět do ri a změnit párovací hrany na nepárovací a naopak, což znamená aktualizování záznamů v polích par_r, (par_s) pro všechny vrcholy na nalezené cestě. Funkce Zlepsi bude volána opakovaně v cyklu tak dlouho, dokud bude možné zvyšovat počet hran v párování. Podaří-li se vylepšit párování n krát, máme nalezeno perfektní párování, které použijeme na přerovnání matice do požadovaného tvaru. V opačném případě program podá zprávu o tom, že se zadaná matice uspořádat nedá.
Efektivita
Každé volání funkce Zlepsi potřebuje čas O(n2), celkově se provede nejvýše n volání této funkce, což dává celkovou časovou složitost O(n3). Na uložení matice A potřebujeme paměť O(n2).
P-I-2
Úlohu nejprve převedeme do terminologie teorie grafů. Uzly nacházející se v naší soustavě potrubí budeme nazývat vrcholy, trubky nazveme hranami a celou soustavu potrubí nazveme grafem. Posloupnost vrcholů a hran grafu v0,e1,v1,e2,...,vk-1ek,vk označíme jako sled, jestliže každá hrana ei spojuje vrcholy vi-1 a vi. Pokud navíc v0 = vk, tento sled nazveme uzavřeným. V řeči teorie grafů je naším úkolem v daném souvislém grafu G nalézt uzavřený sled, který projde každou hranou grafu právě dvakrát.Ukážeme si algoritmus, který v libovolném souvislém grafu najde sled požadovaných vlastností. Tento algoritmus tedy bude zároveň důkazem, že trasa pro robota vždy existuje. Řešení je založeno na prohledávání grafu do hloubky. O každém vrcholu si budeme pamatovat, zda jsme ho již během prohledávání někdy navštívili. Pro každý navštívený vrchol v nechť rodic[v] označuje vrchol, z něhož robot do v poprvé přišel. Vrchol rodic[v] je rodičem vrcholu v, naopak vrchol v nazveme potomkem vrcholu rodic[v]. Pro vrchol 1 není rodic[1] definován.
Prohledávání do hloubky začíná ve vrcholu 1 a probíhá takto:
- Označ aktuální vrchol v jako navštívený.
- Postupně kontroluj všechny hrany vedoucí z v a vždy, když najdeš hranu, která vede do dosud nenavštíveného vrcholu u, projdi robotem do vrcholu u a pokračuj rekurzívně v prohledávání z u (v se stane rodičem vrcholu u).
- Když jsou všechny hrany vedoucí z v zkontrolovány a v<>1, vrať se do vrcholu rodic[v] (a pokračuj v kontrolování jeho hran). Jestliže v=1, skonči.
Podle dosud popsaného prohledávání do hloubky tedy robot navštíví každý vrchol a projde každou stromovou hranou právě dvakrát. Zbývá rozhodnout, kdy a jak bude robot procházet nestromové hrany. Během prohledávání lze snadno detekovat všechny nestromové hrany. Jestliže se robot nachází ve vrcholu u a kontroluje hranu (u,v), tato hrana je nestromová tehdy, pokud vrchol v již byl navštíven a u není rodičem v ani v není rodičem u. Když robot nacházející se ve vrcholu u narazí na nestromovou hranu (u,v), může příslušnou trubku vyčistit tak, že jí projde z vrcholu u do v a zpět.
Implementace algoritmu
Prohledávání do hloubky můžeme snadno implementovat rekurzívní procedurou. Jelikož rekurze si pro aktuální vrchol automaticky pamatuje svého rodiče, není třeba explicitně udržovat záznamy rodic[v]. Graf lze v programu reprezentovat maticí velikosti n x n, z čehož vyplývá časová i paměťová složitost programu O(n2). Při použití efektivnější reprezentace hran spojovým seznamem je možné dosáhnout časové i paměťové složitosti O(m+n), kde m je počet hran grafu, ovšem za cenu o něco komplikovanějšího programu.
P-I-3
Dokážeme nejprve, že spravedlivá přímka vždy existuje. Uvažujme libovolnou orientovanou přímku vedoucí bodem [0,0]. Nechť x je rozdíl počtu bílých bodů nalevo a černých bodů napravo od ní. Jestliže je x rovno nule, přímka je spravedlivá. Pokud ne, budeme přímkou otáčet kolem bodu [0,0]. Vždy, když přímka projde přes bílý nebo černý bod, hodnota x se sníží nebo zvýší o jedna. Když přímku otočíme přesně o 180o, naše sledovaná hodnota se změnila z počátečního x na -x (neboť všechny body, které byly původně nalevo, jsou nyní napravo od přímky a naopak). To znamená, že hodnota musela být aspoň při jedné poloze přímky nulová. V této poloze byla přímka spravedlivá.Řekneme, že bod B leží nalevo od bodu A, jestliže je nalevo od orientované přímky vedoucí z bodu [0,0] do A. Základem algoritmu je následující pozorování. Uvažujme nějakou spravedlivou přímku p. Nechť A je první bod, na který narazíme, pokud budeme přímkou p otáčet ve směru hodinových ručiček kolem bodu [0,0]. Bod A a všechny body, které leží od něj napravo, se nacházejí v jedné polorovině určené přímkou p. Body, které jsou od A nalevo, leží ve druhé polorovině. Vidíme, že nezáleží na konkrétní poloze přímky p, rozdělení bodů je určeno polohou "hraničního" bodu A.
Stačí tedy uvažovat každý ze zadaných bodů jako kandidáta na bod A, spočítat počet bílých a počet černých bodů nalevo a napravo od něj a zkontrolovat, zda tyto počty splňují podmínky spravedlivé přímky. Když najdeme úspěšného kandidáta, spravedlivou přímku sestrojíme tak, že přímku vedoucí z [0,0] tímto bodem trochu pootočíme kolem bodu [0,0] proti směru hodinových ručiček tak, abychom s ní při tomto otáčení nepřešli přes žádný jiný bod. To lze provést například tak, že určíme první bod X, přes který bychom při takovémto otáčení přímkou přešli, a výslednou přímku vedeme středem mezi kandidátem A a bodem X. Popsaný algoritmus má časovou složitost O(n2), neboť pro každého kandidáta zjišťujeme polohu každého bodu vzhledem k tomuto kandidátovi.
Algoritmus lze ještě zefektivnit tím, že si všechny bílé a černé body nejprve setřídíme podle jejich pořadí ve směru hodinových ručiček kolem bodu [0,0]. Kandidáty na hraniční bod A pak budeme zkoušet v tomto utříděném pořadí. Kdykoliv budeme přecházet od kandidáta i-1 ke kandidátovi i, nemusíme již pro každý bod znovu zjišťovat, zda leží od bodu i nalevo nebo napravo, neboť mnoho bodů zůstane v původní polorovině. Budeme si proto v každém kroku udržovat informaci o počtu bílých a černých bodů ležících v pravé polorovině a index j, který ukazuje na poslední bod v pravé polorovině ve směru hodinových ručiček. Když se přesuneme na kandidáta i, stačí bod i-1 přemístit do levé poloroviny (tj. odebrat ho z počtu bodů příslušné barvy, které jsou v pravé polorovině) a potom posouvat index j ve směru hodinových ručiček, dokud nenajdeme první bod, který leží nalevo od bodu i. Všechny body, přes které jsme s indexem j přešli, se přesunou z levé poloroviny do pravé a je proto třeba připočítat je k zaznamenanému počtu bodů příslušné barvy. Pokud při posouvání bodu j dojdeme na konec pole, budeme pokračovat cyklicky opět od začátku. Nesmíme zapomenout ošetřit okrajové případy, když například všechny body leží od bodu j nalevo nebo napravo.
Utřídit body ve směru hodinových ručiček můžeme v čase O(n log n) některým ze standardních třídicích algoritmů, pouze namísto běžného porovnávání hodnot si musíme napsat funkci, jež pro dva body určí, který z nich má větší úhel. Pro první bod musíme projít všechny ostatní body a zjistit, které leží vlevo a které vpravo (v čase O(n)). Pro každý další bod už jen budeme posouvat indexy i a j a sledovat pouze body, přes které přecházíme. Přes každý bod přejdeme každým indexem nejvýše jednou, takže celkový čas posouvání pro všechny kandidátské body dohromady bude O(n). Výsledná časová složitost algoritmu bude proto O(n log n) a paměťová složitost O(n).
P-I-4
Část a
Vstupní soubor může mít například následující formát (váš program samozřejmě může používat jiný formát vstupních dat). Na prvním řádku souboru je zadán počet vodičů a počet komparátorů v síti, na druhém řádku jsou uvedeny jednotlivé vstupy sítě v pořadí od vrchního vodiče po spodní a zbývající řádky obsahují popis sítě. Každý komparátor je určen dvěma čísly zapsanými na jednom řádku. Tato čísla udávají vrchní a spodní vodič, které jsou spojené příslušným komparátorem. Vodiče v síti jsou očíslovány shora dolů počínaje jedničkou. Komparátory jsou uvedeny v pořadí zleva doprava, jednotlivé vrstvy sítě se oddělují řádkem obsahujícím dvě nuly.Program může pro jednoduchost zobrazovat výpočet sítě semigraficky. Nejprve přečte vstupní údaje, přičemž informace o všech komparátorech a oddělovačích vrstev uloží do jednoho pole. Potom bude vykreslovat síť postupně zleva doprava. Pokaždé, když program nakreslí komparátor, odsimuluje jeho činnost na aktuálním stavu vodičů. To znamená, že porovná příslušné dvě hodnoty v poli a pokud jsou v opačném pořadí, vymění je. Po ukončení každé vrstvy (tj. vždy, když v seznamu komparátorů narazíme na oddělovač vrstev) program vypíše aktuální stav hodnot na všech vodičích.
Jediný problém, který je třeba vyřešit, spočívá v umístění jednotlivých komparátorů téže vrstvy do sloupců pod sebe tak, aby se žádné dva komparátory v jednom sloupci nepřekrývaly. Program si proto bude pamatovat, které z vodičů jsou v aktuálním sloupci už obsazeny komparátorem. Jestliže se další komparátor překrývá s některým komparátorem zakresleným v aktuálním sloupci, založíme nový sloupec a komparátor umístíme do nového sloupce.
Celková časová složitost takto navrženého programu je úměrná velikosti nakresleného obrázku, tj. O(nk), kde n je počet vodičů a k je počet sloupců, v nichž jsou komparátory zobrazeny.
Vstup
Výstup
Část b
Komparátorovou síť sestrojíme rekurzívně. Označme Sn síť, která úlohu řeší pro n vstupů. Síť S1 neobsahuje žádný komparátor, neboť máme jen jeden vstup a ten je jistě setříděn. Předpokládejme, že n>1. První vrstva sítě obsahuje pouze jediný komparátor umístěný mezi vodiči n a n/2. Potom rozdělíme n vodičů na dvě poloviny -- horní a dolní -- a na každou polovinu vodičů použijeme síť Sn/2. Tyto dvě podsítě budou pracovat paralelně.Konstrukce sítě Sn je zobrazena na následujícím obrázku vlevo, vpravo je příklad výsledné sítě pro n=8.
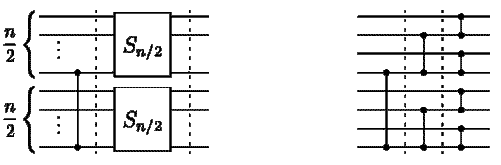
Ukážeme si, proč takto sestavená síť řeší zadanou úlohu.
Postupujeme indukcí podle počtu vodičů. Označme vstupní hodnoty
sítě x1,x2,...,xn (umístěny na vodičích v pořadí shora
dolů). Mohou nastat dva případy podle toho, zda je xn menší
nebo větší než xn/2. Předpokládejme nejprve, že xn >=
xn/2. V takovém případě komparátor v první vrstvě nevymění
vstupní hodnoty. Protože xn >= xn/2, prvek xn patří
v uspořádaném pořadí na některý z dolní poloviny vodičů.
("Dolní" polovinou vodičů budeme rozumět vodiče se vstupními
hodnotami xn/2+1 až xn, tzn. vodiče, které na schématu
komparátorové sítě kreslíme v dolní polovině obrázku.)
Po prvním kroku výpočtu tedy platí, že horní polovina je celá utříděna a obsahuje n/2 nejmenších prvků ze vstupu. Dolní polovina je utříděna s případnou výjimkou posledního prvku a obsahuje n/2 největších prvků. Vstupy obou podsítí Sn/2 tudíž splňují podmínku ze zadání, že všechny hodnoty kromě poslední mají být na vstupu utříděny (to nevylučuje případ, že také poslední hodnota bude utříděna). Na výstupu proto budou podle indukčního předpokladu obě poloviny v setříděném pořadí. Jelikož už po prvním kroku každá polovina obsahovala správné prvky, bude správně uspořádána i celá posloupnost.
Druhý případ nastane, jestliže xn < xn/2. V této situaci komparátor v první vrstvě vymění hodnoty obou těchto vodičů. Víme, že xn patří někam do horní poloviny prvků a dostane se na nejspodnější vodič horní poloviny. Naopak, poslední prvek z horní poloviny, tj. xn/2, patří ve skutečnosti do dolní poloviny (při třídění je "vytlačen" prvkem xn). Prvek xn/2 se však prvním komparátorem dostane na nejspodnější vodič, tj. do dolní poloviny. Podobně jako v předchozím případě i nyní tedy máme po prvním kroku v každé polovině ty prvky, které tam v setříděném pořadí patří. Obě poloviny jsou navíc setříděny s případnou výjimkou svého nejspodnějšího prvku. Po aplikování podsítí Sn/2 proto opět podle indukčního předpokladu dostaneme dvě utříděné poloviny, které společně vytvoří celou správně uspořádanou posloupnost.
Hloubka rekurze je v naší konstrukci log2 n, neboť každá úroveň rekurze sníží počet vodičů na polovinu. V každé úrovni rekurze přidáme do sítě jednu vrstvu, celkový počet vrstev je tedy také roven log2 n.
První vrstva obsahuje jeden komparátor, v každé další vrstvě se počet komparátorů zdvojnásobí. Nechť počet vstupů je n=2k. Potom počet použitých komparátorů je roven 1+2+4+...+2k-1=2k-1=n-1 (součet geometrické řady). Naše síť má tedy O(log n) vrstev a používá O(n) komparátorů.