Matematická olympiáda – kategorie P
Zadání úloh oblastního kola 50. ročníku
Druhé kolo 50. ročníku MO kategorie P se koná v úterý 9. 1. 2001 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého času. Řešení každého příkladu musí obsahovat (není-li v zadání některé úlohy uvedeno jinak):- Popis řešení,to znamená slovní popis použitého algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu).
- Program. V úlohách P-II-1, P-II-2 a P-II-3 je třeba uvést dostatečně podrobný zápis algoritmu, nejlépe ve tvaru zdrojového textu nejdůležitějších částí programu v jazyku Pascal nebo C. Ze zápisu můžete vynechat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů apod. V úloze P-II-4 uveďte místo zdrojového textu zápis dlaždicového programu.
Se správným řešením úloh oblastního kola se můžete seznámit krátce po soutěži na Internetu na stránkách olympiády http://mo.mff.cuni.cz/. Na stejném místě bude po vyhodnocení uveden také seznam úspěšných řešitelů, kteří postoupili do celostátního kola soutěže.
Váš program na vstupu obdrží celé číslo N (počet tyček) a
dále N navzájem různých kladných čísel d1 až dN (délky tyček).
Úkolem vašeho programu je určit počet trojic i<j<k
takových, že čísla di, dj a dk splňují trojúhelníkovou nerovnost,
tj. di<dj+dk, dj<di+dk a dk<di+dj.
Robot se má pohybovat v obdélníkové místnosti, na jejíž podlaze je
nakreslena čtvercová síť. Na některých políčkách v místnosti jsou
postaveny překážky - na tato políčka nesmí robot během svého pohybu
vstoupit. Robot se bude po místnosti pohybovat pouze rovnoběžně
s některou ze stěn.
Společnost však trpí i nedostatkem schopných techniků, a
tak jsou možnosti pohybu robota po místnosti značně limitovány.
Robot rozpoznává celkem tři příkazy: Krok, Doleva a Doprava.
Při obdržení příkazu Krok se robot přesune na sousední
políčko v tom směru, ve kterém je právě natočen. Při obdržení příkazu
Doleva se otočí o 90 stupňů doleva a při obdržení Doprava se
otočí o 90 stupňů doprava.
Vaším úkolem je vytvořit program, který jako vstup dostane rozměry
čtvercové sítě na podlaze místnosti (M a N), souřadnice políčka,
na kterém se robot právě nachází, a souřadnice políčka, na které se má robot
přesunout. Souřadnice políček číslujeme od 1, první souřadnice
udává řádek, druhá sloupec. Levý horní roh místnosti má souřadnice
[1,1] (viz příklad níže). Každý z následujících M řádků obsahuje N
čísel 0 nebo 1. Je-li j-té číslo na i-tém řádku 1,
pak na políčku se souřadnicemi [i,j] je překážka, pokud je toto
číslo 0, pak se na políčku se souřadnicemi [i,j] překážka
nenachází. Úkolem je nalézt a vypsat posloupnost příkazů,
podle nichž robot dojde z počátečního políčka na cílové.
Věc má však ještě jeden háček: Provedení příkazů Doleva a
Doprava je časově velmi náročné a vámi vytvořená posloupnost instrukcí
pro pohyb robota v místnosti by měla obsahovat co nejmenší počet
těchto dvou příkazů. Počet příkazů Krok může být libovolný. Počáteční
natočení robota si můžete zvolit. V případě, že robot nemůže přejít
z počátečního na cílové políčko, vypište vhodnou zprávu.
Navrhněte co nejefektivnější algoritmus, který dostane na vstupu
počet vrcholů původního obrazu n, počet Pepíčkových střihů k a popis
jednotlivých střihů a na základě těchto údajů určí počet vrcholů té zbylé
části, která jich má nejvíce. Každý střih je popsán dvojicí čísel (ai, bi), což
jsou čísla vrcholů v původním n-úhelníku, mezi kterými Pepíček střih vedl.
Vrcholy n-úhelníka jsou číslovány po obvodu po řadě čísly od 1 do n.
Snažte se, aby časová ani paměťová složitost vašeho řešení nezávisela na
počtu vrcholů obrazu.
Nejprve několik definic: Dlaždice jsou stejně velké čtverce
s obarvenými hranami. Konkrétnímu přiřazení barev hranám dlaždice
budeme říkat typ dlaždice a budeme jej zapisovat jako uspořádanou
čtveřici (l,p,h,d) udávající barvu v pořadí levé, pravé, horní a
dolní hrany. Abychom si usnadnili práci, budeme barvy označovat
různými symboly - písmeny, čísly apod. Dlaždice typu (1,2,3,4)
bude tedy vypadat následovně:
Abychom se nemuseli zabývat tím, jak přesně velkou zeď máme zvolit pro
ten či onen vstup úlohy, budeme šířku zdi volit vždy stejnou, jako
je délka vstupu (horní okraj tedy bude celý zaplněn vstupem), zatímco
výšku zdi použijeme nejmenší, pro níž existuje vydláždění s použitím
naší sady dlaždic.
Když tento způsob počítání srovnáme s klasickým programováním, zjistíme,
že zvolená sada dlaždic tvoří v našem modelu něco podobného programu a potřebná
výška zdi vzdáleně odpovídá době běhu výpočtu - budeme se proto
snažit, aby u našich řešení byla co nejmenší.
Formálně řečeno, dlaždicový program je uspořádaná čtveřice D=(T,l0,p0,d0),
kde T je konečná množina typů dlaždic {(l1,p1,h1,d1),...,
(lk,pk,hk,dk)} a l0, p0 a d0
jsou okrajové barvy. Rozhodovací úlohou P(x) rozumíme úlohu
zjistit, zda vstup x (konečná posloupnost symbolů, resp. barev z předem
určené konečné množiny) má požadovanou vlastnost P. Říkáme, že dlaždicový
program řeší rozhodovací úlohu P(x), jestliže platí,
že P(x)=
Myšlenka našeho řešení je velice jednoduchá: sestrojíme sadu dlaždic, která
bude umožňovat právě taková vydláždění, v nichž v každém řádku přepíšeme
právě jedno sudé a jedno liché číslo na "kolečko". Dolní okraj zdi obarvíme
též barvou "kolečko". Jelikož obarvení spodního okraje je vyvážené
a vydláždění každého řádku vyváženost zachovává, pak jakákoliv vstupní posloupnost,
pro kterou vydláždění existuje, je opravdu vyvážená. A naopak: pokud máme
vyváženou posloupnost, pak snadno ověříme, že vydláždění existuje: vybereme
si libovolné sudé a libovolné liché číslo (z vyváženosti víme, že v posloupnosti taková dvojice je),
ta jedním řádkem dlaždic přepíšeme na "kolečko" a toto opakujeme tak dlouho
(n/2-krát), dokud nebudou všechna čísla přepsána.
Pokud se nám tedy podaří takový dlaždicový program sestrojit, bude zadanou úlohu řešit
se složitostí O(n).
P-II-1 Trojúhelníky
Pepík našel na půdě u babičky krabici s dřevěnými tyčkami. Začal si s nimi
hrát a sestavovat z nich trojúhelníky různých tvarů. Uviděl ho jeho tatínek a
začalo ho zajímat, kolik různých trojúhelníků lze z těchto tyček sestavit.
Vaším úkolem je pomoci mu s nalezením odpovědi na tuto otázku.Příklad
Pro N=5 a d1=5.5, d2=1.5, d3=2.0, d4=2.5, d5=7.5
váš program odpoví číslem 2, neboť trojúhelník lze sestavit
pouze z trojice tyček o délkách d1, d4 a d5 a dále z trojice
o délkách d2, d3 a d4. Všimněte si, že trojice tyček o délkách
d1, d3 a d5 netvoří trojúhelník.P-II-2 Robot
Společnost pro Rovnoprávnost robotů a lidí se snaží vyvinout robota,
který by se mohl sám pohybovat v místnosti s překážkami.
Bohužel této společnosti chybí softwarový expert a proto se rozhodla,
že vás požádá o pomoc.Příklad
Představme si místnost se čtvercovou sítí 4x8 z následujícího
obrázku:
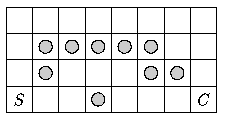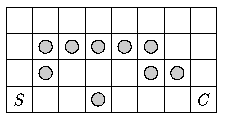
Úkolem je přesunout robota z políčka označeného S (o souřadnicích [4,1])
na políčko označené C (o souřadnicích [4,8]). Vstup vašeho programu by
tedy vypadal následovně:
Krok Krok Krok Doprava Krok Krok Krok Krok Krok Krok Krok Doprava Krok Krok Krok
Při této cestě robot udělá 13 kroků a dvakrát se otočí; všimněte si též
existence cesty s 9 kroky a 4 otočeními - tato cesta je sice kratší,
ale podle zadání úlohy není optimální, neboť se během ní robot musí
otočit vícekrát.P-II-3 Pepíček
Malému Pepíčkovi se jednoho dne dostaly do ruky nůžky. A protože byl Pepíček
tvořivý po tatínkovi, jenž byl moderním malířem, rozhodl se vylepšit jeden jeho
obraz ve tvaru konvexního n-úhelníka. Vybral si dva vrcholy tohoto
n-úhelníka a obraz přestřihl po spojnici těchto dvou vrcholů. Pak si na jedné
ze vzniklých částí opět vybral dva vrcholy a část opět přestřihl. Když si takto
Pepíček chvilku hrál, přistihl ho tatínek, nůžek ho nekompromisně zbavil a
začal zachraňovat, co se dá. Po chvilce zjistil, že obraz dohromady už nesloží.
Rozhodl se tedy, že alepoň nalezne zbylou část s největším počtem vrcholů a tu
vystaví na své nadcházející výstavě jako miniaturu. A právě s hledáním mu máte
pomoci vy.Příklad
Pro n=10, k=3 a střihy (1,8), (7,5) a (4,2) má největší část 6 vrcholů.P-II-4 Dlaždice
(Definice dlaždicových programů je stejná jako v domácím kole, pouze
příklad jejich použití je složitější a ukazuje, jak je možno využívat
více řádků dlaždic.)

Prostor, který budeme dláždit (budeme mu říkat zeď), má tvar
obdélníku o velikosti m x n (m i n jsou přirozená čísla;
jednotkou délky budiž délka hrany dlaždice). Strany obdélníku jsou
rozděleny na úseky jednotkové délky a každému úseku je opět přiřazena
barva. Naším cílem je pokrýt zeď dlaždicemi tak, aby v každém
z m x n jednotkových čtverců zdi byla umístěna právě jedna
dlaždice, sousední dlaždice se dotýkaly vždy hranami téže barvy a
rovněž krajní dlaždice přiléhaly k okraji zdi vždy hranou takové
barvy, jakou má i příslušný úsek okraje zdi. Dlaždice není povoleno
otáčet.Příklad
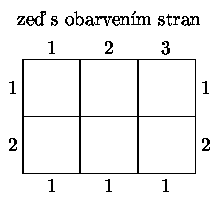
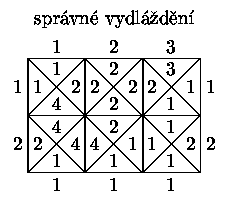

Pomocí dláždění můžeme snadno řešit úlohy, jejichž výsledkem je buďto odpověď
ano nebo ne: sestavíme vhodnou množinu typů dlaždic (ta je
pro daný problém pevná - nezávisí na vstupu), vezmeme
vhodně velkou zeď, její horní okraj obarvíme podle vstupu našeho problému,
ostatní okraje ponecháme jednobarevné a budeme se ptát, zda je tuto zeď
možno vydláždit či nikoliv. Přitom chceme, aby tento výsledek byl
shodný s řešením naší úlohy.ano právě tehdy, když existuje v>0
takové, že je možno vydláždit dlaždicemi typů obsažených v množině T
zeď velikosti |x| x v s horní hranou obarvenou
vstupem x a levou, pravou a dolní hranou obarvenou po řadě barvami
l0, p0 a d0. Od každého typu je možno použít libovolně mnoho
dlaždic. Složitostí programu D pro daný vstup x nazveme nejmenší v, pro něž
to je možné; pokud takové neexistuje, a tedy P(x)=ne,
definujeme složitost jako nulovou. Složitost programu je funkce délky
vstupu n, jejíž hodnota udává maximum ze složitostí programu pro jednotlivé
vstupy této délky.Příklad
Zkonstruujme dlaždicový program, který bude ověřovat, zda je daná posloupnost
tvořená přirozenými čísly x1,...,xn (0<=xi<=9) vyvážená,
tzn. zda obsahuje stejný počet sudých a lichých čísel.
Hledaný program může vypadat například následovně: Použijeme následující
typy dlaždic:
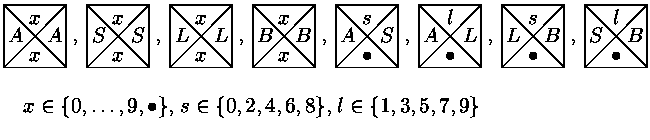
Levý okraj obarvíme barvou A, pravý barvou B a dolní barvou "kolečko".
Z těchto dlaždic je možno konstruovat výhradně řádky typu:

kde xi je sudé a xk liché, případně

pro xi liché a xk sudé. To jsou přesně řádky, jaké jsme potřebovali.Soutěžní úloha
Sestrojte dlaždicový program, který o dané posloupnosti přirozených čísel
x1,x2,...,xn (0<= xi <= 9) rozhodne, zda je symetrická, tj. zda x1=xn, x2=xn-1,
..., xi=xn-i+1, ..., xn=x1.