Matematická olympiáda – kategorie P
Řešení úloh ústředního kola (1. soutěžní den) 50. ročníku
P-III-1 Věže
Nejdříve je třeba si uvědomit, že jednotlivé souřadnice pozic věží je možno volit nezávisle na sobě. To platí proto, že volba sloupce nijak neomezí rozsah řádek, ve kterém může být věž umístěna. Můžeme tedy nejdříve pro každou věž zvolit sloupec, ve kterém se bude nacházet, a pak pro každou věž zvolit řádek. Převedli jsme tak původní úlohu do jednoho rozměru. Jednotlivé obdélníky se promítnou na intervaly a v každém intervalu chceme nalézt číslo i (umístění věže) takové, aby se čísla žádných dvou intervalů neshodovala.Čísla budeme hledat následujícím způsobem: Budeme postupně procházet čísla od 1 do N a budeme si udržovat informaci, které intervaly obsahují dané číslo a ještě nemají žádné číslo přiděleno. Z těchto intervalů vybereme ten, který končí nejdříve, a přidělíme mu aktuální číslo. Pokud vybraný interval již neobsahuje přidělované číslo (skončil dříve), úloha nemá řešení. Přímá implementace této myšlenky je samozřejmě možná, ale pomalá (O(N2)). My implementaci zrychlíme následujícím způsobem: Abychom mohli rychle upravovat informace o tom, které intervaly obsahují dané číslo, setřídíme si je nejdříve vzestupně podle jejich počátku. Abychom byli dále schopni rychle nalézt interval, který končí nejdříve, budeme si intervaly obsahující dané číslo uchovávat v haldě srovnané podle konců intervalů. Přidělování čísel tedy ve vylepšené implementaci probíhá následovně: Procházíme všechna čísla od 1 do N. Pro každé číslo přidáme do haldy všechny intervaly začínající na daném čísle. Pak z haldy (pokud je neprázdná) odebereme minimum (tj. nejdříve končící interval) a přidělíme mu aktuální číslo. Pokud interval již neobsahuje aktuální číslo, řekneme, že požadované rozestavení věží neexistuje. S těmito vylepšeními má algoritmus časovou složitost O(N log N) a paměťovou složitost O(N).
Nechť máme nějaké korektní rozestavení věží R. Indukcí dokážeme, že toto rozestavení lze upravit na takové, jaké navrhne náš algoritmus, a tím tedy ukážeme, že náš algoritmus nalezne korektní rozestavení věží.
- Počátek indukce: Nechť C je nejmenší číslo, které náš algoritmus chce přidělit nějakému (vlastně prvnímu) intervalu I. Z chování našeho algoritmu je zřejmé, že v žádném rozestavení se nižší číslo vyskytovat nemůže. Pokud se v R nevyskytuje ani číslo C, můžeme R upravit tak, že I dáme číslo C. Tím jistě získáme korektní rozestavení, které navíc má pro první interval I přiděleno stejné číslo, jaké by navrhl náš algoritmus. Pokud je v R číslo C již přiděleno nějakému intervalu J, můžeme snadno intervalu J přidělit číslo přidělené intervalu I a intervalu I přiřadit C. Protože interval I končil dříve než interval J, jistě máme opět korektní rozestavení.
- Indukční krok: Z indukčního předpokladu víme, že existuje rozestavení, které se shoduje s rozestavením navrhovaným naším algoritmem v prvních k číslech. Chceme ukázat, že existuje rozestavení, které se shoduje v prvních k+1 číslech. Protože myšlenka důkazu je naprosto stejná jako v počátku indukce, necháváme tuto část důkazu na čtenáři.
P-III-2 Nuly a jedničky
Nejprve ukážeme, že pro každé přirozené číslo N existuje přirozené číslo x, jehož ciframi jsou pouze číslice 0 a 1 a které je dělitelné číslem N. Označme x1=1, x2=11, x3=111 atd. Dále označme jako mi číslo xi mod N. Čísla mi mohou nabývat pouze hodnot od 0 do N-1 a proto alespoň dvě z čísel m1 až mN+1 musí být stejná - nechť např. mi=mj (i<j). Potom ale číslo xj-xi je dělitelné číslem N, neboť (xj-xi) mod N=mj-mi=0. Ciframi čísla xj-xi jsou zřejmě pouze číslice 0 a 1 a tedy číslo xj-xi splňuje podmínky ze zadání úlohy.Nadále budeme uvažovat pouze ta čísla, jejichž dekadický zápis je tvořen pouze číslicemi 0 a 1. Předchůdcem čísla x nazveme číslo x div 10, tedy číslo x bez své poslední cifry; naopak následníky čísla x nazveme čísla 10x a 10x+1, tedy ta čísla, která lze vytvořit přidáním jedné cifry na konec čísla x. Číslo x budeme nazývat minimálním číslem pro zbytek z, jestliže x mod N=z, v dekadickém zápisu čísla x se vyskytují pouze číslice 0 a 1 a x je nejmenší číslo s těmito vlastnostmi. Nyní si dokážeme jednoduché lemma:
Lemma
Nechť x je minimální číslo pro zbytek z, nechť x' je předchůdcem x; označme z'=x' mod N. Potom x' je minimální číslo pro zbytek z'.Důkaz
Postupujme sporem, tedy předpokládejme, že x' není minimální číslo pro zbytek z', tj. že existuje číslo x''Tímto postupem lze vygenerovat minimální čísla pro všechny zbytky, pro které existují: Položme l1=1 a pokud už známe l1,...,lk, položme lk+1 rovno nejmenšímu následníkovi některého z čísel l1,...,lk takovému, že lk+1 mod N je různý od všech li mod N pro 1<=i<=k. Z předchozích úvah ale vyplývá, že jednotlivá čísla li jsou minimální čísla pro zbytky zi=li mod N. Navíc podle prvního odstavce je jedno z čísel zi rovno nule.
Náš algoritmus bude pracovat přesně podle výše uvedeného popisu. V poli fronta si budeme pamatovat hodnoty zi a na m-té pozici v poli predchozi si budeme pamatovat zbytek předchůdce od minimálního čísla pro zbytek m - z hodnot v tomto poli jsme schopni jednoduše zkonstruovat minimální číslo pro zadaný zbytek. Postupně budeme brát hodnoty zi z pole fronta, spočítáme (10*zi) mod N a (10*zi+1) mod N a pokud jsme dosud nenašli číslo, jehož zbytek by byla jedna z těchto hodnot, tak tento zbytek přidáme na konec pole fronta a příslušně zmodifikujeme pole predchozi. Časová a paměťová složitost algoritmu je zřejmě O(N).
P-III-3 Dlaždice
Abychom nemuseli vše popisovat zbytečně složitě, zaveďme si jednoduché značení: Posloupnosti budou vždy složeny jen z nul a jedniček a všechny budou mít n prvků. Budeme je značit tučnými písmeny a jejich prvky písmeny s indexy, tedy například x je posloupnost obsahující prvky x1,...,xn. Počtu jedniček v posloupnosti x budeme říkat její váha a značit #x.Posloupnost y je setříděním posloupnosti x právě tehdy, když platí současně následující dvě podmínky:
- y1 <= ... <= yn (je to neklesající posloupnost)
- #y=#x (x a y obsahují stejný počet jedniček a jelikož mají stejnou délku, tak i stejný počet nul, čili se navzájem liší pouze pořadím prvků)
Zabývejme se nejprve tím, jak ověřit druhou podmínku. Mohli bychom postupovat podobně, jako u příkladu v zadání oblastního kola: v každém řádku vydláždění odstranit po jedné jedničce z obou posloupností, a to opakovat tak dlouho, až obě posloupnosti budou obsahovat pouze nuly, což snadno ověříme barvou spodního okraje zdi. Tím úlohu vyřešíme s lineární složitostí, což ovšem, jak si ukážeme, není optimální. U myšlenky postupného "zjednodušování" testovaných posloupností však zůstaneme:
Tvrzení
#x=#y => #x mod 2 = #y mod 2 a #x'=#y', kde x' je posloupnost, která vznikne z posloupnosti x přepsáním každé druhé jedničky na nulu (to jest přepsáním první jedničky, ponecháním druhé, přepsáním třetí, ponecháním čtvrté atd.).Důkaz
Pokud #x=#y, pak jistě #x mod 2 = #y mod 2, ale jelikož #x'=[#x/2] (v x' zbyla právě polovina jedniček z x, případná lichá jednička na konci byla odstraněna), musí platit i #x'=#y'. A naopak: pokud #x'=#y', mohou se posloupnosti x a y lišit pouze případnou lichou poslední jedničkou, což ovšem není možné, protože váhy #x a #y jsou buďto obě liché nebo obě sudé.
Vytvořme nejprve dlaždicový podprogram, který pro danou posloupnost x zadanou
barvami horního okraje spočte x' na okraji dolním a #x mod 2
na okraji pravém (v tom smyslu, že vydláždění bude existovat právě tehdy, když barvy
těchto okrajů splňují dané podmínky, a toto vydláždění bude mít jediný řádek), předpokládaje,
že levý okraj má barvu 0.
K tomu nám poslouží následující množina T0 typů dlaždic:
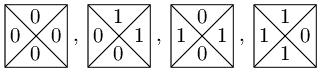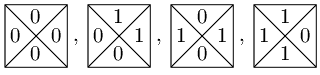
Označíme-li si zi barvu pravé hrany a yi barvu dolní hrany i-té dlaždice
vydlážděného řádku (z0 budiž barva levé hrany první dlaždice, tedy barva
levého okraje zdi, což je 0), snadno ukážeme, že:
- zi = (x1+...+xi) mod 2 ... Indukcí: pro i=0 platí, pro i>0 je zi=(zi-1+xk) mod 2=((x1+...+xi-1) mod 2 + xi) mod 2 =(x1+...+xi) mod 2.
- yi=1 <=> xi=1 & zi-1=1, jinými slovy právě tehdy, je-li xi jednička, před níž byl lichý počet jedniček, čili jednička sudá - právě ta, která se má objevit v x'.
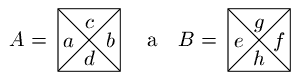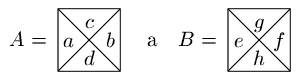
do T1 přidáme následující dlaždici:

kde ae, bf, cg a dh jsou uspořádané dvojice barev. Existuje-li vydláždění řádku, který má na horní hraně dvojice (x1,y1),...,(xn,yn), na dolní hraně (x'1,y'1),...,(x'n, y'n), na levé (0,0) a na pravé (zx,zy), dlaždicemi typů z množiny T1, musí díky tomu, jak jsme si tyto typy nadefinovali, existovat i vydláždění řádku s horní hranou x1,...,xn, dolní x'1,...,x'n, levou 0 a pravou zx, jakož i řádku s horní hranou y1,...,yn, dolní y'1,... y'n, levou 0 a pravou zy dlaždicemi typů T0. A opačně -- existují-li tato dvě vydláždění, existuje i jejich složení sestavené z typů z množiny T1. Proto zx=#x mod 2, zy=#y mod 2 a spodní hrana opravdu obsahuje dvojice prvků posloupností x' a y'.
My ovšem potřebujeme akceptovat právě ta vydláždění, u nichž zx=zy,
tedy s pravým okrajem jak (0,0), tak (1,1), ale máme k dispozici pouze
jedinou barvu pravého okraje zdi. Proto rozšíříme množinu T1 na T2
tak, že ke každému typu dlaždice z T1 tvaru
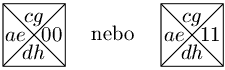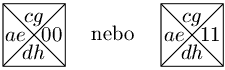
přidáme do T2 následující typ:

kde P je barva pravého okraje, která se neshoduje s žádnou jinou barvou.
Jelikož se tato dlaždice může vyskytnout výhradně těsně u pravého okraje
(žádná dlaždice totiž nemá levou hranu barvy P, na kterou bychom mohli
navázat), odpovídají korektní vydláždění pomocí této rozšířené sady dlaždic
právě těm vydlážděním pomocí původní sady, u nichž je zx=zy.
Zbývá nám ještě přidat test vzestupnosti posloupnosti y, což vyřešíme
přidáním dlaždic následujících typů:
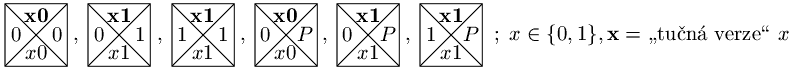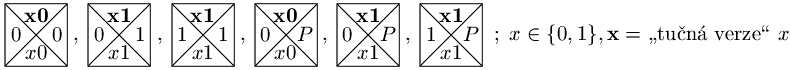
kde 00, 01, 10 a 11 jsou barvy dvojic kódujících
zadané posloupnosti x a y a 00, 01, 10 a 11 analogické
kódy používané všemi ostatními dosud nadefinovanými dlaždicemi. Tím z T2
vznikne množina typů T, o které tvrdíme, že použita s barvou levého okraje
0, barvou pravého P a barvou dolního okraje 00, řeší zadanou úlohu se
složitostí O(log n), což také ihned dokážeme:
- První řádek vydláždění musí obsahovat výhradně dlaždice typů Tz, protože žádné jiné neobsahují na svých horních hranách barvy, jimiž je kódován vstup. Jak jsme již ukázali v příkladu v zadání domácího kola, typy Tz zajišťují neklesání posloupnosti y. Navíc spodní okraj tohoto řádku předává níže obě vstupní posloupnosti, pouze jinak kódované.
- Všechny ostatní řádky obsahují pouze dlaždice typů T2, přičemž každý řádek přepíše posloupnosti xi a yi zadané na svém horním okraji na xi+1=x'i a yi+1=y'i a ověří, zda #xi mod 2 = #yi mod 2. Pokud #x=#y, pak po maximálně [log2n] takových řádcích budou obě posloupnosti zredukovány na samé nuly, což odpovídá barvě dolního řádku, čili vydláždění celé zdi existuje a má hloubku <= 1+[log2n]; pokud #x<>y, vydláždění nemůže existovat, protože alespoň v jednom kroku by #xi mod 2 nebylo rovno #yi mod 2 (viz Tvrzení výše).
Poznámka
Lepší hloubky než log n již není možno dosáhnout. To můžeme zdůvodnit podobně, jako jsme v předchozím kole dokazovali, že pro ověření symetrie posloupnosti potřebujeme hloubku minimálně lineární. Opět budeme počítat možná obarvení středního sloupce -- tentokráte si uvědomíme, že tato obarvení musí být rozdílná pro každé dva různé počty jedniček v x1,...,xn/2 -- pokud jsou jedničky pouze mezi těmito prvky a xn/2+1,...,xn jsou všechny nulové, musí setříděná posloupnost y obsahovat naopak ve své levé polovině samé nuly a v polovině pravé stejný počet jedniček, jako má x v polovině levé. Možných počtů jedniček mezi x1,...,xn/2 je n/2+1, možných obarvení středního sloupce <= bh, kde b je počet barev použitých v našem dlaždicovém programu (to je nějaká konstanta) a h je jeho složitost = výška středního sloupce. Z toho dostaneme:bh >= n/2 + 1 > n/2
h > logb n - logb 2