Matematická olympiáda – kategorie P

Řešení úloh školního kola 50. ročníku

Tento pracovní materiál není určen primárně přímo studentům - účastníkům olympiády. Má pomoci učitelům na školách při přípravě konzultací a pracovních seminářů pro řešitele soutěže, členům oblastních výborů MO slouží jako podklad pro opravování úloh domácího kola MO kategorie P. Studentům je možné tyto komentáře poskytnout až po termínu stanoveném pro odevzdání řešení úloh domácího kola MO kategorie P jako informaci, jak bylo možné úlohy správně řešit, a pro jejich odbornou přípravu na účast v oblastním kole soutěže.

P-I-1 Stromy

Je jasné, že za každé dva uzly hloubky K, K>0 musí existovat jeden uzel hloubky K-1, který není listem - každé dva uzly musíme pod nějaký uzel "zavěsit". Protože navíc pod každý uzel můžeme zavěsit pouze žádný nebo dva uzly, musí být počet uzlů hloubky K sudý. Výše uvedená pozorování nám již dávají návod na sestrojení algoritmu. Pro každou hloubku si budeme pamatovat počet listů a počet ostatních uzlů. Budeme postupovat od uzlů s největší hloubkou. Pro každou hloubku K, K>0 zkontrolujeme, zda je počet uzlů v ní sudý. Pokud není, strom neexistuje. Pokud je počet uzlů sudý, za každé dva uzly umístěné ve stromu na dané hloubce přidáme do předchozí hloubky jeden uzel. Když se takto dostaneme až k uzlům hloubky 0, stačí ověřit, jestli v této hloubce leží právě jeden uzel, jak je vyžadováno v definici binárního stromu. Pokud není, strom neexistuje. To plyne z toho, že pokud neexistuje uzel hloubky 0, nebyl dán žádný list, a tedy strom nemůže mít žádné uzly. To je ale ve sporu s požadavkem, že každý strom musí mít alespoň kořen. Pokud je uzlů hloubky 0 naopak více, strom neexistuje, protože všechny uzly, které jsme přidávali, byly vynucené a každý strom s danými počty listů tedy musí mít na jednotlivých hloubkách alespoň tolik uzlů jako náš strom. Pokud existuje právě jeden uzel hloubky 0, snadno již ze spočítaných počtů listů a ostatních uzlů v jednotlivých hloubkách vytvoříme požadovaný zápis stromu. Jednoduše vypíšeme tolik L, kolik je počet listů dané hloubky, a tolik U, kolik je počet ostatních uzlů dané hloubky. Algoritmus má časovou i paměťovou složitost O(N). Program je přímou implementací algoritmu.

program STROMY; const MAXV = 10000; var Vrcholu : Array[0..MAXV, 1..2] of Word; {Počty listů a nelistů jednotlivých hloubek} V : Word; {Počet listů} Existuje : Boolean; {Může zadaný strom existovat?} procedure Vstup; {Načte vstup ze souboru} var Inp : Text; i, H : Word; begin Assign(Inp, 'stromy.in'); Reset(Inp); ReadLn(Inp, V); for i := 1 to V do begin Vrcholu[i,1] := 0; Vrcholu[i,2] := 0; end; for i := 1 to V do begin Read(Inp, H); if H >= V then begin Existuje := False; break; end; Inc(Vrcholu[H,1]); end; Close(Inp); end; procedure Vypis(Existuje : Boolean); {Vypíše nalezený strom či případně zprávu o jeho neexistenci} var Out : Text; i,j : Word; begin Assign(Out, 'stromy.out'); Rewrite(Out); if Existuje then for i := 0 to V-1 do begin for j := 1 to Vrcholu[i,2] do Write(Out, 'U'); for j := 1 to Vrcholu[i,1] do Write(Out, 'L'); WriteLn(Out); end else WriteLn(Out, 'Odpovidajici strom neexistuje.'); Close(Out); end; function NajdiStrom : Boolean; {Pokusí se nalézt strom s danými hloubkami listů} var i : Word; begin {Projdeme všechny možné hloubky listů} for i := V-1 downto 0 do begin {Je počet vrcholů na nějaké úrovni lichý?} if (Vrcholu[i+1,1] + Vrcholu[i+1,2]) mod 2 = 1 then begin Existuje := False; {Úroveň nad námi nemůže být korektní ...} break; end; {Vždy pod každým vrcholem visí právě dva vrcholy} Vrcholu[i,2] := (Vrcholu[i+1,1] + Vrcholu[i+1,2]) div 2; end; {Je na první úrovni více než jeden vrchol?} if Existuje and (Vrcholu[0,1] + Vrcholu[0,2] > 1) then Existuje := False; end; begin Existuje := True; Vstup; if Existuje then NajdiStrom; Vypis(Existuje); end.

P-I-2 Posel

Algoritmus řešící tuto úlohu se dá rozdělit do tří fází. V první fázi se pro každé město spočítá, jaká je jeho vzdálenost od nepřítelem obsazených měst (ve smyslu definice uvedené v zadání). Ve druhé fázi se zjistí, jakou maximální vzdálenost od nepřátelských měst dokážeme udržet při cestě z počátečního do cílového města. Ve třetí fázi pak nalezneme nejkratší z tras vedoucích z počátečního do cílového města, které udržují spočtenou vzdálenost.

První fáze: Vzdálenost od obsazených měst budeme hledat pomocí prohledávání do šířky. U každého města si budeme udržovat informaci, zda jsme v něm již byli (na počátku bude nastaveno právě u všech obsazených měst) a jeho vzdálenost od nepřítele. Pro města obsazená nepřítelem bude tato vzdálenost rovna 0. Dále si budeme udržovat frontu měst ke zpracování, do které na začátku uložíme všechna nepřátelská města. V každém kroku výpočtu vždy vezmeme jedno město z fronty a u všech jeho sousedů, ve kterých jsme dosud nebyli, nastavíme vzdálenost o jedna větší, než je vzdálenost vybraného města. U všech těchto sousedů také označíme, že jsme v nich už byli, a přidáme je na konec fronty. První fáze výpočtu končí, když se vyprázdní fronta. Tehdy jsme prošli všechna města a určili jsme vzdálenost každého z nich od nepřítele.

Druhá fáze: V této fázi si budeme udržovat front hned několik, pro každou vzdálenost od nepřátelských měst jednu. Dále si pro každé město budeme zaznamenávat, zda jsme v něm už byli. Také si budeme pamatovat dosud největší nalezenou vzdálenost, kterou dokážeme udržet od nepřítele. Na začátku nastavíme udržitelnou vzdálenost od nepřítele na hodnotu vzdálenosti královského města od nepřítele a toto město vložíme do fronty pro příslušnou vzdálenost. U tohoto města také nastavíme, že jsme v něm už byli. Výpočet probíhá tak, že postupně vyzvedáváme města z fronty pro aktuální udržitelnou vzdálenost, dokud se tato fronta nevyprázdní. Když se fronta vyprázdní, snížíme udržitelnou vzdálenost o jedna a opět začneme vybírat města z příslušné fronty. Vždy, když vezmeme nějaké město z fronty, projdeme všechny jeho sousedy, u dosud nenavštívených z nich nastavíme příznak, že už jsme je nenavštívili, a přidáme je do fronty - jestliže je vzdálenost takového města od nepřátelských měst větší, než je aktuální udržitelná vzdálenost, přidáme vrchol do fronty odpovídající aktuální udržitelné vzdálenosti, jinak město přidáme do fronty odpovídající jeho vzdálenosti od nepřátelských měst. Druhá fáze končí, jakmile vybereme z fronty cílové město. Aktuální udržitelná vzdálenost je pak výslednou udržitelnou vzdáleností.

Třetí fáze: Tato fáze představuje opět prosté prohledávání do šířky. Pro každé město si pamatujeme, zda jsme v něm již byli, a pokud ano, zaznamenáme si také město, ze kterého jsme do něj přišli. Opět používáme frontu na dosud nezpracovaná města. Na začátku vložíme do fronty cílové město. U něj nastavíme, že jsme v něm již byli, a jako jeho předchůdce nastavíme je samé. V každém kroku výpočtu pak vezmeme jedno město z fronty a projdeme všechny jeho sousedy. Každého souseda, kterého jsme dosud nenavštívili a jehož vzdálenost od nepřátelských měst je větší nebo rovna výsledné udržitelné vzdálenosti, označíme jako navštíveného a přidáme ho na konec fronty. Také u něj jako město, ze kterého jsme přišli, nastavíme právě vybrané město. Prohledávání končí ve chvíli, když je z fronty vyzvednuto počáteční (královské) město. Poté už jenom projdeme cestu z počátečního do cílového města (to je velmi snadné díky odkazům na města, odkud jsme do nich při prohledávání přišli) a cestu vypíšeme.

Algoritmus má časovou složitost O(M+N), kde M je počet cest a N je počet měst.

Správnost algoritmu budeme ukazovat opět po fázích. To, že algoritmus spočte správně vzdálenosti od nepřátelských měst v první fázi, plyne z následujícího: Na počátku mají všechny vrcholy se vzdáleností nula tuto vzdálenost přiřazenu. V okamžiku, kdy jsou zpracovány všechny vrcholy vzdálenosti nula, prošli jsme všechny jejich sousedy, přiřadili jsme jim vzdálenost jedna a zařadili je do fronty. Protože jiné vrcholy vzdálenost jedna mít nemohou, je vzdálenost jedna přiřazena právě všem správným vrcholům. Tuto úvahu lze snadno zobecnit pro libovolnou vzdálenost D. Prohledávání tedy skutečně určí vzdálenosti od nepřátelských měst správně.

Ve druhé fázi se správně spočítá maximální udržitelná vzdálenost od obsazených měst. Sledujeme v ní totiž souběžně všechny možné trasy vedoucí z počátečního města tak dlouho, dokud dokážeme udržet vzdálenost počátečního města (výsledná vzdálenost od nepřítele zřejmě nemůže být větší než vzdálenost počátečního města). Když už neexistuje město s dostatečně velkou vzdáleností, do kterého bychom mohli jít, snížíme udržitelnou vzdálenost o jedna. Všechny vrcholy se vzdáleností o jedna nižší, do kterých se dokážeme dostat přes vrcholy s dosavadní udržitelnou vzdáleností, máme již připraveny v příslušné frontě a začneme tedy prohledávat z nich. Protože udržitelnou vzdálenost snižujeme až když jsme se již dostali všude, kam to bylo možné, její výsledná hodnota bude zřejmě nejvyšší možná.

To, že ve třetí fázi nalezneme nejkratší trasu s danou vzdáleností, je zřejmé. Provádíme totiž jednoduché prohledávání do šířky s tím, že ignorujeme města s příliš malou vzdáleností od nepřítele. Nalezneme tedy určitě trasu s dostatečnou vzdáleností od nepřítele. Skutečnost, že to bude trasa nejkratší možná, plyne z vlastností prohledávání do šířky uvedených v první části důkazu.

Program je přímou implementací uvedeného algoritmu.

program POSEL; const MAXV = 100; {Maximální počet měst} type MestT = record Byl : Boolean; {Navštívili jsme již při posledním prohledávání toto město} HC : Byte; {Počet cest z daného města} H : Array[1..MAXV] of Byte; {Sousedi daného města} NepritelD : Byte; {Vzdálenost od města obsazeného nepřítelem} end; MestP = Array[1..MAXV] of Byte; {Typ pro pole s čísly měst} var VC : Byte; {Počet měst} V : Array[1..MAXV] of MestT; {Jednotlivá města} NVC : Byte; {Počet měst obsazených nepřítelem} NV : MestP; {Čísla měst obsazených nepřítelem} Start, Cil : Byte; {Počáteční a cílové město} procedure Nacti; var Inp : Text; i : Word; M : Word; {Počet všech existujících cest} A, B : Byte; {Počáteční a koncové město cesty} begin Assign(Inp, 'posel.in'); Reset(Inp); Read(Inp, VC); for i := 1 to VC do V[i].HC := 0; ReadLn(Inp, M); for i := 1 to M do begin ReadLn(Inp, A, B); {Přidáme cestu k oběma městům} Inc(V[A].HC); V[A].H[V[A].HC] := B; Inc(V[B].HC); V[B].H[V[B].HC] := A; end; {Načteme obsazená města} ReadLn(Inp, NVC); for i := 1 to NVC do Read(Inp, NV[i]); {Načte počáteční a cílové město} Read(Inp, Start); ReadLn(Inp, Cil); Close(Inp); end; procedure NeprVzdal; {Spočítá vzdálenost jednotlivých měst od nepřátelských} var S, N : Byte; {První a poslední město ve frontě} F : Array[1..MAXV] of Byte; {Fronta měst} A : Byte; {Aktuální město} I : Byte; begin {Inicializujeme hodnoty Byl} for i := 1 to VC do begin V[i].Byl := False; V[i].NepritelD := VC; end; N := 0; S := 1; {Naplníme frontu nepřátelskými městy} for i := 1 to NVC do begin Inc(N); F[N] := NV[i]; V[NV[i]].Byl := True; V[NV[i]].NepritelD := 0; end; {Dokud je něco ve frontě} while N >= S do begin A := F[S]; Inc(S); for i := 1 to V[A].HC do begin if not V[V[A].H[i]].Byl then begin {Nastavíme vzdálenost od nepřítele} V[V[A].H[i]].Byl := True; V[V[A].H[i]].NepritelD := V[A].NepritelD + 1; {Přidáme město do fronty} Inc(N); F[N] := V[A].H[i]; end; end; end; end; function ZjistiMinVzdal : Byte; {Zjistí, jakou vzdálenost si dokážeme udržet od nepřítele} var S : Array[1..MAXV] of Byte; {Počátky jednotlivých front} N : Array[1..MAXV] of Byte; {Poslední města v jednotlivých frontách} F : Array[1..MAXV, 1..MAXV] of Byte; {Fronty} A : Byte; {Aktuální město} ActD : Byte; {Aktuální vzdálenost od nepřítele} I : Byte; begin for i := 1 to VC do begin S[i] := 1; N[i] := 0; V[i].Byl := False; end; {Uložíme do fronty počáteční město} Inc(N[V[Start].NepritelD]); F[V[Start].NepritelD,N[V[Start].NepritelD]] := Start; V[Start].Byl := True; {Projdeme všechny možné vzdálenosti} for ActD := V[Start].NepritelD downto 0 do begin {Dokud je ve frontě něco ke zpracování} while S[ActD] <= N[ActD] do begin A := F[ActD,S[ActD]]; if A = Cil then begin {Nalezli jsme cestu až do cílového města?} ZjistiMinVzdal := ActD; break; end; Inc(S[ActD]); for i := 1 to V[A].HC do begin if not V[V[A].H[i]].Byl then begin {Ještě jsme v tomto městě nebyli?} V[V[A].H[i]].Byl := True; if V[V[A].H[i]].NepritelD >= ActD then begin {Můžeme do něj vejít teď?} {Přidáme město do fronty} Inc(N[ActD]); F[ActD,N[ActD]] := V[A].H[i]; end else begin {Do města teď vstoupit nemůžeme} {Přidáme ho do příslušné fronty do budoucna} Inc(N[V[V[A].H[i]].NepritelD]); F[V[V[A].H[i]].NepritelD,N[V[V[A].H[i]].NepritelD]] := V[A].H[i]; end; end; end; end; if A = Cil then break; end; end; procedure VypisCestu(Prev : MestP); {Vypíše nalezenou trasu} var A : Byte; {Aktuální město} Out : Text; begin Assign(Out, 'posel.out'); Rewrite(Out); {Projdeme celou nalezenou trasu} A := Start; while A <> Cil do begin Write(Out, A, ' '); A := Prev[A]; end; WriteLn(Out, A); Close(Out); end; procedure NajdiCestu(D : Byte); {Nalezne nejkratší trasu přes města vzdálenosti alespoň D} var S, N : Byte; {Počátek a konec fronty} F : Array[1..MAXV] of Byte; {Fronta na města} Prev : MestP; {Města, odkud jsme přišli} A : Byte; {Aktuální město} i : Byte; begin for i := 1 to VC do V[i].Byl := False; {Zařadíme počáteční město do fronty} S := 1; N := 1; F[N] := Cil; V[Cil].Byl := True; Prev[Cil] := Cil; while S <= N do begin {Vyzvedneme město z fronty} A := F[S]; if A = Start then break; Inc(S); for i := 1 to V[A].HC do {Projdeme všechny cesty z města} {Ještě jsme v daném městě nebyli a je dost daleko od nepřátel?} if (not V[V[A].H[i]].Byl) and (V[V[A].H[i]].NepritelD >= D) then begin {Zařadíme město do fronty} V[V[A].H[i]].Byl := True; Inc(N); F[N] := V[A].H[i]; Prev[V[A].H[i]] := A; {Poznamenáme, odkud jsme přišli} end; end; VypisCestu(Prev); {Vypíšeme nalezenou cestu} end; begin Nacti; {Načte vstup} NeprVzdal; {Spočte vzdálenosti od nepřítele} {Zjistí, jakou vzdálenost dokážeme mít od nepřítele a nalezne nejkratší cestu} NajdiCestu(ZjistiMinVzdal); end.

P-I-3 Výlet

Řešení úlohy rozdělíme na několik částí - nejprve zformulujeme nutné a postačující podmínky pro to, aby skupina mohla projet trasu dle podmínek v zadání úlohy, poté vyřešíme úlohu a) a nakonec nalezneme řešení úlohy b).

Plánovanou trasu lze projet právě tehdy, když tato trasa není delší než vzdálenost, kterou skupina urazí za den, tj. L<=K, anebo když jsou splněny zároveň všechny čtyři následující podmínky:

• Na trase je alespoň jeden kemp.
• Vzdálenost prvního kempu od začátku trasy je nejvýše K, tj. l₁<=K.
• Vzdálenost libovolných dvou po sobě následujících kempů není větší než K, tj. l_i+1-l_i<=K pro 1<=i<=N-1.
• Vzdálenost posledního kempu od konce trasy je nejvýše K, tj. L-l_N<=K.

Nutnost všech uvedených podmínek je zřejmá; pokud jsou tyto podmínky splněny, pak plán cesty, ve kterém skupina bude cestovat N+1 dní a i-tý den přespí v i-tém kempu, splňuje podmínky ze zadání úlohy.

Nyní vyřešíme úlohu a). Na chvíli si představme, že jsme každému kempu přiřadili číslo d_i, které udává, kolikátý den nejdříve můžeme do tohoto kempu dorazit. Číslo d_i přiřazené kempu i zřejmě splňuje jednu z následujících dvou podmínek:

• Buď je d_i=1 a l_i<=K - do kempu lze dorazit hned první den.
• Existuje j<i takové, že l_i-l_j<=K a d_j=d_i-1 (do i-tého kempu dorazíme tak, že den před tím přespíme v j-tém kempu), ale neexistuje j<i takové, že l_i-l_j<=K a d_j<d_i-1 (jinak by bylo možné do j-tého kempu dorazit již dříve).

Podle těchto podmínek by bylo možné spočítat všechna d_i v čase O(N), náš program však d_i počítat nebude. Plán cesty splňující podmínku a) by mohl vypadat například tak, že h-tý den skupina přespí v i-tém kempu, pokud d_i=h a d_i+1=h+1; skupina navíc přespí v N-tém kempu, pokud plán cesty bez tohoto kempu nesplňuje podmínku omezující maximální vzdálenost, kterou lze urazit za jeden den. Budeme přímo vytvářet takovýto plán cesty -- pokud dosud vytvořený plán cesty končí kempem ve vzdálenosti l od začátku výletu a L-l>K (nelze bez přespání dorazit na konec trasy), pak další den skupina přespí v i-tém kempu, pokud l_i-l<=K a i je maximální s touto vlastností. Vytvořit program pracující podle právě popsaného postupu je triviální; časová složitost algoritmu je O(N).

Dále vyřešíme úlohu b). Každému kempu přiřadíme číslo e_i, které udává, kolik by cyklisté museli zaplatit za přespání na cestě z i-tého kempu na konec výletu (počítáno včetně poplatku za přespání v i-tém kempu). Čísla e_i náš algoritmus spočítá postupně pro i=N až i=1; kromě těchto čísel, si pro každý z kempů uložíme informaci, do kterého následujícího kempu se z něj máme vydat, abychom za noclehy zaplatili optimální cenu e_i. Čísla e_i lze spočítat podle následujícího předpisu:

1. Pokud L-l_i<=K, potom e_i=c_i; z i-tého kempu lze dorazit na konec trasy během jednoho dne.
2. Pokud L-l_i>K, potom e_i=min_j (c_i+e_j)=c_i+min_j e_j, kde se minimum počítá přes všechna j>i taková, že l_j-l_i<=K; to j, pro které se nabývá minima, určuje pořadí kempu, ve kterém přespíme ten den, kdy vyjedeme z i-tého kempu.

První den, pokud L>K, přespíme v kempu s číslem i s minimálním e_i, pro který platí l_i<=K. Jak bude algoritmus pracovat je nyní již jasné. Zbývá ještě určit, jak rychle lze najít j, které minimalizuje vztah v druhém bodě.

K rychlému nalezení indexu j, použijeme datovou strukturu, která se nazývá halda. Halda je datová struktura, která umožňuje v konstantním čase určit nejmenší z prvků v haldě; prvek do haldy přidat nebo vyjmout nejmenší prvek umí v čase logaritmickém v počtu prvků obsažených v haldě. V haldě si budeme udržovat čísla kempů setříděná podle hodnot e_i; na začátku budeme mít v haldě navíc konec trasy, jehož hodnotu budeme považovat za rovnu nule (bude nejmenším prvkem haldy). Nalezení vhodného j bude probíhat následovně: Zjistíme, zda nejmenší prvek haldy je od i-tého kempu vzdálený nejvýše o K - pokud ano, nalezli jsme příslušné j, v opačném případě z haldy odstraníme tento prvek a celý postup zopakujeme. Poté do haldy přiřadíme i-tý kemp. Za předpokladu logaritmického času přidání prvku do haldy a vyjmutí nejmenšího prvku z haldy je celková doba běhu algoritmu O(N log N).

Haldu budeme reprezentovat v poli. Bude-li v haldě n prvků, pak její prvky budou uloženy v poli na pozicích s čísly 0 až n-1. Pro prvek x s indexem k budeme prvky na pozicích 2k+1 a 2k+2 nazývat syny prvku x a prvek x budeme nazývat otcem těchto prvků. Všimněte si, že každý prvek, mimo prvku na pozici 0, má právě jednoho otce. Při práci s haldou budeme dodržovat následující invariant: Každý prvek je větší než jeho otec. Nejmenším prvkem v haldě je proto prvek na nulté pozici; zjištění nejmenšího prvku haldy lze tedy provést v konstantním čase. Přidání prvku do haldy bude probíhat následovně: Je-li v haldě n prvků, pak nový prvek umístíme na pozici n; pokud je jeho otec větší, vyměníme přidávaný prvek s jeho otcem a celý postup opakujeme tak dlouho, dokud nový prvek není nultým prvkem nebo jeho otec není menší než on. V každém kroku se index nového prvku v poli zmenší alespoň na polovinu a tedy se po logaritmicky mnoha krocích zastavíme. Odebrání prvku z haldy bude probíhat podobně: Je-li v haldě n prvků, pak nejmenší prvek haldy nahradíme prvkem z (n-1)-té pozice; tento prvek porovnáme s oběma jeho syny a popřípadě ho zaměníme s menším z obou jeho synů. Skončíme, pokud je tento prvek menší než oba jeho synové. Protože se v každém kroku posuneme na prvek s alespoň dvojnásobným indexem, odebrání nejmenšího prvku z haldy bude trvat čas logaritmický v počtu prvků v haldě.

program vylet; const MAXN=10000; var l: array[1..MAXN] of lognint; { vzdálenosti kempů } c: array[1..MAXN] of word; { ceny za nocleh } delka: word; { celková délka výletu } K: word; { maximální vzdálenost pro jeden den } N: word; { počet kempů } f: text; function ma_reseni:boolean; var i: word; begin if (delka<=K) then ma_reseni:=true else begin ma_reseni:=false; if (l[1]>K) then exit; for i:=1 to N-1 do if (l[i+1]-l[i]>K) then exit; if (delka-l[N]>K) then exit; ma_reseni:=true; end end; procedure vyres_a; var opt: array[1..MAXN] of word; { optimální řešení } optpocet: word; { počet kempů v poli opt } optcena: word; { cena za přespání v kempech dle pole opt } vzdalenost: word; { vzdálenost posledního kempu v poli opt } i: word; begin vzdalenost:=0; optpocet:=0; optcena:=0; i:=1; while (i<N) do begin if (l[i+1]-vzdalenost>K) then begin inc(optpocet); opt[optpocet]:=i; inc(optcena,c[i]); vzdalenost:=l[i]; end; inc(i) end; if (delka-vzdalenost>K) then begin inc(optpocet); opt[optpocet]:=i; inc(optcena,c[i]); end; assign(f,'VYLET-A.OUT'); rewrite(f); writeln(f,optpocet,' ',optcena); for i:=1 to optpocet do writeln(f,opt[i]); close(f) end; procedure vyres_b; var halda: array[0..MAXN] of word; { pomocná halda } vhalde: word; { velikost pomocné haldy } optcena: array[0..MAXN] of word; { minimální cena cesty z daného kempu do konce trasy } nasledujici: array[0..MAXN] of word; { následující kemp na opt. trase } { Označení: 1 až N - kempy, 0 - konec trasy } function cena(p:word):word; { vrací opt. cenu cesty z kempu p do konce trasy } begin if p=0 then cena:=0 else cena:=optcena[p] end; function vzdalenost(p:word):word; { vrací vzdálenost kempu p } begin if p=0 then vzdalenost:=delka else vzdalenost:=l[p] end; procedure vyjmi; { vyjme nejmenší prvek z haldy } var i, j, k: word; begin dec(vhalde); halda[0]:=halda[vhalde]; i:=0; while (((i shl 1)+1<vhalde) and (cena(halda[i])>cena(halda[(i shl 1)+1]))) or (((i shl 1)+2<vhalde) and (cena(halda[i])>cena(halda[(i shl 1)+2]))) do begin j:=i; { vybereme větev, do které půjdeme } if (((i shl 1)+1<vhalde) and (cena(halda[j])>cena(halda[(i shl 1)+1]))) then j:=(i shl 1)+1; if (((i shl 1)+2<vhalde) and (cena(halda[j])>cena(halda[(i shl 1)+2]))) then j:=(i shl 1)+2; { ... a zaměníme prvky } k:=halda[i]; halda[i]:=halda[j]; halda[j]:=k end end; procedure pridej(p:word); { přidá kemp p do haldy } var i, j, k: word; begin i:=vhalde; halda[i]:=p; inc(vhalde); while (i>0) and (cena(halda[i])<cena(halda[(i-1) shr 1])) do begin j:=(i-1) shr 1; k:=halda[j]; halda[j]:=halda[i]; halda[i]:=k; i:=j end end; var i,j: word; begin vhalde:=1; halda[0]:=0; for i:=n downto 1 do begin while (vzdalenost(halda[0])-l[i]>K) do vyjmi; optcena[i]:=c[i]+cena(halda[0]); nasledujici[i]:=halda[0]; pridej(i); end; while (vzdalenost(halda[0])>K) do vyjmi; optcena[0]:=cena(halda[0]); nasledujici[0]:=halda[0]; { spočítáme počet kempů na cestě } i:=0; j:=0; while (nasledujici[i]<>0) do begin inc(j); i:=nasledujici[i]; end; { vypíšeme řešení } assign(f,'VYLET-B.OUT'); rewrite(f); writeln(f,j,' ',optcena[0]); i:=0; while (nasledujici[i]<>0) do begin i:=nasledujici[i]; writeln(f,i); end; close(f) end; var i: word; begin assign(f,'VYLET.IN'); reset(f); readln(f,delka,K,N); for i:=1 to N do readln(f,l[i],c[i]); close(f); if not ma_reseni then begin assign(f,'VYLET-A.OUT'); rewrite(f); writeln(f,'Trasu nelze projet.'); close(f); assign(f,'VYLET-B.OUT'); rewrite(f); writeln(f,'Trasu nelze projet.'); close(f); end else begin vyres_a; vyres_b; end end.

P-I-4 Dlaždice

1. Mějme zadáno nějaké dvojkové číslo <x₁,...,x_n>, o němž máme rozhodnout, zda je dělitelné pěti. Sestrojíme sadu dlaždic, jíž bude možno vydláždit pouze zeď o jednom řádku, a to tak, aby barva pravé hrany i-té dlaždice (tu budeme značit p_i) odpovídala zbytku po dělení dvojkového čísla <x₁,...,x_i> pěti. Když navíc zvolíme barvu pravého okraje zdi tak, aby odpovídala zbytku 0, půjde zeď vydláždit právě tehdy, je-li zadané číslo dělitelné pěti, a to je přesně to, co potřebujeme.
   Použijeme dlaždice následujících typů:
   
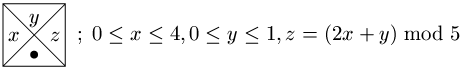
   Levý i pravý okraj budou mít barvu 0 a dolní okraj barvu "kolečko". Jelikož barva "kolečko" se nevyskytuje na horní hraně žádné dlaždice, musí být každé korektní vydláždění tvořeno jediným řádkem. Zbývá dokázat, že barvy pravých hran dlaždic odpovídají zbytkům, což učiníme indukcí:
   • p₁=<x₁>=<x₁> mod 5 (existuje právě jedna dlaždice, která může být na prvním políčku - ta, která má na levém okraji nulu a na horním okraji x₁).
   • Je-li p_i=<x₁,...,x_i> mod 5, může být na i+1-ním políčku pouze jediná dlaždice (mající na levém okraji p_i a na horním okraji x_i+1) a její pravý okraj má barvu p_i+1=(2p_i+x_i+1) mod 5= (2(<x₁,...,x_i> mod 5)+x_i+1) mod 5= (2<x₁,...,x_i>+x_i+1) mod 5 =<x₁,...,x_i+1> mod 5.
   Z toho plyne, že popsaný dlaždicový program řeší zadanou úlohu se složitostí O(1).

2. Použijeme následující typy dlaždic:
   
   • "Levé" dlaždice:
     
     
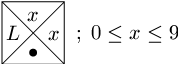
   • "Pravé" dlaždice:
     
     
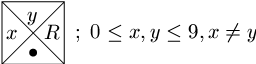
   • "Opakovací" dlaždice:
     
     
   Levý okraj zdi obarvíme barvou L, pravý barvou R a spodní barvou "kolečko". Jelikož barva "kolečko" se nevyskytuje na horní hraně žádné dlaždice, musí být každé korektní vydláždění tvořeno jediným řádkem.
   Z toho, jak jsme si typy dlaždic nadefinovali, ihned plyne, že každé vydláždění zdi musí vypadat takto:
   
   Zleva doprava: nejprve (možno i prázdná) posloupnost dlaždic opakujících L, pak jedna levá dlaždice, následuje opět několik opakovacích dlaždic, jedna pravá dlaždice a případně opakování R. Takové vydláždění je ovšem korektní právě tehdy, bylo-li možné nalézt indexy i a j takové, že x_i<>x_j (díky definici barev hran pravé dlaždice), takže náš dlaždicový program řeší zadanou úlohu se složitostí O(1).

Poznámka

Naše řešení využívá toho, že dlaždicové programy jsou nedeterministické (to znamená, že nemají pevně definovaný průběh výpočtu a místo toho připouštějí více různých výpočtů s tím, že odpovědí programu je ano, pokud existuje alespoň jeden korektní výpočet) a že nám nedeterminismus "uhodne" polohu nějakých dvou různých prvků vstupní posloupnosti.