Matematická olympiáda – kategorie P

Zadání úloh školního kola 49. ročníku

Řešení každého příkladu musí obsahovat popis použitého algoritmu, zdůvodnění jeho správnosti a diskusi o efektivitě zvoleného řešení (tzn. posouzení časových a paměťových nároků programu).

V praktických úlohách P-I-1 a P-I-3 je třeba k řešení připojit odladěný program zapsaný v jazyce Pascal, C nebo C++. Program se odevzdává v písemné formě (jeho výpis je tedy součástí řešení) i na disketě, aby bylo možno otestovat jeho funkčnost. Slovní popis řešení musí být ovšem jasný a srozumitelný i bez toho, že by bylo nutno nahlédnout do zdrojového textu programu.

V úloze P-I-2 se požaduje slovní popis zvoleného postupu řešení včetně použitých programů, na disketu uložte jako přílohu k řešení této úlohy pouze výsledný textový soubor s nalezeným řetězcem.

V úloze P-I-4 je třeba nakreslit také schémata programů pro Minského registrové stroje.

P-I-1

V továrně bude zahájena výroba nového typu výrobku. Výroba je popsána přesným technologickým plánem, jenž stanoví, jaké všechny výrobní operace je třeba vykonat a jak dlouho každá z těchto operací trvá. Pro každou výrobní operaci P je dále znám seznam operací, které musí být provedeny před začátkem operace P (nazveme je předcházející operace).

Majitelé továrny chtějí výrobu zorganizovat tak, aby bylo možné dokončit první nový výrobek v co nejkratším čase. V továrně lze současně provádět libovolný počet výrobních operací, každou operaci je však možné zahájit až po dokončení všech jí předcházejících operací. Jinak mohou být jednotlivé výrobní operace prováděny v jakémkoliv pořadí. Můžete předpokládat, že výroba podle zadaného technologického plánu je možná.

Napište program, který ze vstupního textového souboru TOVARNA.IN přečte technologický plán výroby nového výrobku a do výstupního textového souboru TOVARNA.OUT vypíše nejkratší čas, v jakém lze vyrobit první nový výrobek.

Soubor TOVARNA.IN obsahuje na prvním řádku počet výrobních operací N (N <= 100). Na dalších N řádcích se nacházejí informace o jednotlivých výrobních operacích, na i-tém řádku o operaci číslo i. Informace o každé výrobní operaci se skládá z několika čísel oddělených mezerou. První číslo udává, jak dlouho operace trvá, dále následují čísla předcházejících operací. Řádek je ukončen číslem -1. Pro zhotovení nového výrobku je třeba vykonat všech N zadaných výrobních operací. Jednotlivé operace je možné provádět v libovolném pořadí, každá operace však může být zahájena až po dokončení všech jí předcházejících operací.

Soubor TOVARNA.OUT bude obsahovat jediný řádek, na kterém bude zapsán čas, za jak dlouho od zahájení výroby lze dokončit první nový výrobek.

Příklad

Soubor TOVARNA.IN

4 2 3 -1 3 3 -1 3 -1 1 1 2 -1

Soubor TOVARNA.OUT

7

P-I-2

 Je dána množina A={a1,a2,a3,...,aN} (N >= 1), kterou budeme nazývat abeceda. Prvky abecedy budeme nazývat znaky. Řetězcem nad abecedou A je konečná posloupnost prvků z množiny A (znaků). Vybraný podřetězec vznikne z řetězce vynecháním některých jeho znaků, přičemž pořadí zbývajících znaků řetězce zachováme beze změn. Permutace prvků množiny A je řetězec, v němž se každý prvek množiny A vyskytuje právě jednou.

Příklad

Nechť N=3, A={a,b,c}. Potom z řetězce abcabccb můžeme vytvořit například vybrané podřetězce ab, aac, bbcb, abbb, abc, cab. Z nich pouze abc a cab jsou permutace množiny A.

Soutěžní úloha

Nalezněte co nejkratší řetězec nad abecedou A={a,b,c,...,t} (N=15), který obsahuje všechny permutace prvků množiny A jako vybrané podřetězce a každý znak se v něm vyskytuje nejvýše N-krát. Podrobně popište také způsob, jak jste tento řetězec našli, a přiložte a popište všechny algoritmy a programy, které jste přitom použili. Výsledný řetězec uložte do souboru RETEZEC.TXT.

Příklad

Například pro abecedu A={a,b,c} (N=3) vyhovuje řetězec acbacab, protože se v něm nacházejí všechny permutace abc, acb, bac, bca, cab, cba jako vybrané podřetězce. Zároveň je tento řetězec nejkratším řetězcem nad abecedou A splňujícím tuto podmínku.

P-I-3

V jisté zemi existuje N politických stran. Každá ze stran má mezi obyvatelstvem určité preference, přičemž žádné dvě strany nemají stejné preference. Agentury pro výzkum veřejného mínění dokážou provést průzkum, který pro libovolné dvě politické strany umožňuje přesně zjistit, která z nich má preference nižší a která vyšší. Tento průzkum je však poměrně drahý a dá se použít vždy jen pro dvě vybrané politické strany.

Jedna agentura chce zjistit, která ze stran v zemi má nejvyšší a která nejnižší preference. Bude postupovat tak, že pro různé dvojice stran provede výše popsaný průzkum veřejného mínění. Chce přitom vykonat co nejméně průzkumů.

Napište program, který bude řídit činnost agentury. Tento program nejprve přečte počet stran N (1 <= N <= 100). Strany si pro jednoduchost očíslujeme čísly 1,2...,N. Program potom v cyklu vždy vypíše, pro které dvě strany se má provést průzkum, a následně přečte ze vstupu výsledek tohoto průzkumu - číslo strany s většími preferencemi. Když program tímto způsobem získá dostatek údajů potřebných k tomu, aby určil politické strany s nejvyššími a s nejnižšími preferencemi, vypíše odpověď a skončí.

Dbejte zejména na to, aby váš program dal vždy správnou odpověď a aby použil co nejméně průzkumů. Odhadněte, kolik nejvíce průzkumů může váš program potřebovat pro N stran.

Příklad

Uvedeme příklad činnosti programu pro tři strany, přičemž texty vypisované programem jsou od začátku řádku a odpovědi uživatele jsou zadány v řádcích začínajících znakem >.

Zadej počet stran: > 3 Proveď průzkum 1,2 > 2 Proveď průzkum 1,3 > 3 Proveď průzkum 2,3 > 2 Nejvyšší preference má strana 2, nejnižší 1

P-I-4 Minského registrový stroj

Definice Minského registrového stroje

Minského registrový stroj je jednoduché výpočetní zařízení. K dispozici má několik registrů označených R0, R1, R2,..., přičemž v každém registru může být uloženo jedno libovolně velké nezáporné celé číslo.

Minského registrový stroj může mít jeden nebo více vstupů, jejichž hodnoty jsou na začátku výpočtu uloženy v registrech R1,...,Rk, kde k je počet těchto vstupů. Ostatní registry jsou na začátku výpočtu inicializovány na hodnotu nula. Po skončení výpočtu Minského registrového stroje je výsledkem hodnota uložená v registru R0.

Každý Minského registrový stroj je řízen pevně daným programem. V programu se mohou vyskytovat tyto příkazy:

Registr je určen svým číslem. Číslo registru je v příkazu vždy pevně zadáno, není tedy možné k určení registru použít obsah jiného registru.

Programy budeme zakreslovat do schémat, přičemž zvýšení hodnoty registru Ri budeme značit obdélníkem s nápisem Ri++, snížení hodnoty registru Ri budeme značit obdélníkem s nápisem Ri--, test na nulu v registru Ri značíme oválem s nápisem Ri?. Začátek programu označujeme písmenem Z v kroužku a konec programu písmenem K v kroužku (program může mít i více konců, ale jen jeden začátek). Jednotlivé příkazy jsou pospojovány šipkami, které určují tok řízení programu. Z obdélníka vychází vždy jediná šipka. Z oválu vycházejí dvě šipky, přičemž jedna z nich je označena nulou (po ní pokračuje výpočet tehdy, když byla v testovaném registru nula, v opačném případě výpočet sleduje druhou šipku). Jestliže v programu za sebou následuje několik příkazů zvýšení nebo snížení, můžeme je napsat pod sebe do jednoho obdélníku.

Příklad

Sestrojte stroj, který bude mít na vstupu čísla x a y (uložená v registrech R1 a R2) a který vypočítá jejich součin xy (uloží ho do registru R0).

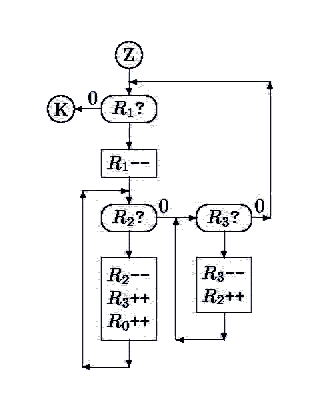
Minského registrový stroj z příkladu

Řešení

Stroj řešící tuto úlohu vidíme na obrázku. Tento stroj vždy odečte od registru R1 jedničku a k registru R0 přičte číslo y (obsah registru R2). To provádí tak dlouho, dokud v registru R1 není nula. Číslo y se tedy do registru R0 přičte celkem x-krát, takže dostaneme správný výsledek.

Podívejme se nyní na to, jak se provádí přičtení čísla y k R0. Opět v cyklu snižujeme hodnotu registru R2 a zvyšujeme hodnotu registru R0, dokud nemáme v registru R2 nulu. Tehdy jsme do R0 přidali přesně y. Problém však spočívá v tom, že v registru R2 máme nyní nulu, ale pro další průběh výpočtu tam potřebujeme vložit zpět hodnotu y. Proto v cyklu kromě snížení R2 a zvýšení R0 ještě zvýšíme R3. Tím si zajistíme, že po skončení cyklu máme hodnotu y uloženou v registru R3. Nyní ji musíme odtamtud přenést zpět do registru R2. To provedeme v dalším cyklu, v němž současně snižujeme R3 a zvyšujeme R2, dokud v R3 není nula. V tom okamžiku máme v R2 opět původní hodnotu y a můžeme začít s dalším kolem výpočtu.

Soutěžní úlohy

  1. Sestrojte Minského registrový stroj s jedním vstupem n, který vypočítá číslo 2n.

  2. Sestrojte Minského registrový stroj s jedním vstupem n, který vypočítá Fibonacciho číslo Fn. Váš stroj přitom může používat pouze registry R0, R1, R2, R3.

Fibonacciho čísla jsou definována následujícím vztahem:
Fn= 1 jestliže n < 2
Fn= Fn-1+Fn-2 jestliže n >= 2