Matematická olympiáda – kategorie P
Zadání úloh školního kola 46. ročníku
Kategorie P matematické olympiády je zaměřena na algoritmizaci a programování. Je určena studentům všech ročníků středních škol.Řešení každého příkladu musí obsahovat popis použitého algoritmu, zdůvodnění jeho správnosti, diskusi o efektivitě zvoleného řešení (tzn. posouzení časových a paměťových nároků programu) a odladěný program. Slovní popis řešení musí být jasný a srozumitelný i bez toho, že by bylo třeba nahlédnout do samotného programu. Program může být napsán v jazyce Pascal nebo C. Odevzdává se s řešením každé úlohy v písemné formě i na disketě, aby bylo možné v případě nejasností otestovat jeho funkčnost. Více řešitelů z téže školy může odevzdat své programy na společné disketě (v tom případě rozdělte soubory jednotlivých řešitelů do podadresářů). Zaslané diskety vám budou po vyhodnocení domácího kola soutěže vráceny zpět.
Řešení úloh domácího kola MO kategorie P studenti zašlou k hodnocení prostřednictvím své školy příslušnému oblastnímu výboru matematické olympiády nejpozději do 10.12.1996.
P-I-1
Napište a odlaďte program na řešení známé "hry 15". V této
hře je ve čtvercové tabulce velikosti 4x4 políčka rozloženo 15
hracích kamenů označených čísly 1,2,...,15. Každý kámen leží
v jednom políčku tabulky, zbývající šestnácté políčko zůstává
prázdné. Povoleným tahem ve hře je přesunutí jednoho kamene na
sousední prázdné políčko v tabulce, a to ve směru svislém nebo
vodorovném. Každý přípustný tah je zřejmě jednoznačně určen
pořadovým číslem políčka, na kterém stál kámen před svým
přesunem. Políčka v tabulce budeme číslovat od 1 do 16 po řádcích
počínaje od levého horního rohu. Například ze situace A můžeme
tahem 6 přejít do situace B:
Situace A
| 7 | 12 | 9 | 3 |
| 15 | 14 | 10 | |
| 1 | 8 | 13 | 5 |
| 11 | 6 | 2 | 4 |
Situace B
| 7 | 12 | 9 | 3 |
| 15 | 14 | 10 | |
| 1 | 8 | 13 | 5 |
| 11 | 6 | 2 | 4 |
Situace K
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 |
Na začátku hry jsou hrací kameny rozloženy v tabulce náhodně. Cílem hry je dosáhnout pomocí povolených tahů koncové situace K, v níž jsou kameny uspořádány po řadách podle čísel a prázdné políčko je v pravém dolním rohu.
Program přečte ze souboru P-I-1.INP počáteční situaci jako
posloupnost čísel kamenů oddělených mezerami (prázdné políčko je
označeno číslem 0). Například situace A by byla popsána vstupní
posloupností 7 12 9 3 15 14 0 10 1 8 13 5 11 6 2 4. Pokud
koncová situace není pomocí povolených tahů dosažitelná, program
vypíše do výstupního souboru P-I-1.OUT zprávu Nemá řešení.
Jestliže koncová situace je dosažitelná, program uloží do
výstupního souboru P-I-1.OUT jednu (kteroukoliv) posloupnost
povolených tahů, která vede ke koncové situaci K. Kromě toho
program vykreslí celou tabulku hry a pomocí semigrafiky nebo
v grafickém režimu znázorní posloupnost tahů vedoucí do koncové
situace. Toto vykreslení by mělo být interaktivně krokovatelné -
například po každém stisku mezerníku by se měl na obrazovce
provést jeden tah výsledné posloupnosti.
Příklady vstupu a výstupu:
P-I-2
Řekneme, že množina bodů M v rovině je schodovitá, jestliže pro každou dvojici (x1, y1), (x2, y2) jejích bodů platí:(x1 <> x2) & ((x1 < x2) => (y1 > y2))
Tzn. jestliže body množiny M uspořádáme podle první souřadnice, dostaneme "klesající" posloupnost.
Řekneme, že dvě neprázdné disjunktní množiny bodů A, B v rovině jsou separovatelné (oddělitelné), jestliže existuje přímka, která rozdělí rovinu na dvě poloroviny tak, že v každé polorovině se nacházejí jen body jedné z množin. Oddělující přímka může obsahovat body jen jedné množiny (případně na ní neleží žádný bod množin A, B).
Na vstupu jsou zadány dvě neprázdné disjunktní schodovité množiny bodů A a B. Vytvořte co nejefektivnější algoritmus a napište program, který zjistí, zda jsou množiny bodů A, B separovatelné. Pokud obě množiny jsou separovatelné, program určí jejich oddělující přímku.
Vstupní soubor P-I-2.INP obsahuje nejprve řádek se dvěma
celými kladnými čísly M a N, která udávají počty prvků množin A,
B. Potom následuje M řádků, z nichž každý obsahuje dvě reálná
čísla - souřadnice jednotlivých bodů množiny A. Dalších N řádků
stejného tvaru udává souřadnice bodů množiny B. Seznamy bodů
množin A a B jsou uspořádány vzestupně podle hodnot první
souřadnice. Můžete předpokládat, že vstupní data jsou zadána
korektně.
Výstupem programu (v souboru P-I-2.OUT) je jeden řádek
obsahující tři reálná čísla A, B, C oddělená mezerami. Tato čísla
představují koeficienty některé oddělující přímky Ax + By +
C =0. V případě, že oddělující přímka neexistuje, výstupem je
trojice čísel 0 0 0.
Příklady vstupu a výstupu
P-I-2.INP
P-I-2.OUT
P-I-2.INP
P-I-2.OUT
P-I-3
Orient-expres projíždí N různými státy (předpokládejme N < 100). Státy si pro jednoduchost očíslujeme od 1 do N v tom pořadí, jak jimi orient-expres projíždí. Každý stát má svou vlastní měnu (měny také očíslujeme, stát L má měnu L). Měny jsou mezi sebou volně směnitelné s tím, že ve státě L můžeme nakupovat jakékoliv jiné měny, ale vždy jen za měnu L. Cestujeme ze státu I do státu J (I < J), takže potřebujeme nakoupit měnu J. Kladné reálné číslo K[I,J] určuje, kolik jednotek měny J dostaneme při přímé výměně za jednu jednotku měny I. Někdy ale mohou být výhodnější nepřímé obchody: vyměníme měnu I za L a potom měnu L za J (I < L < J), příp. I za L, L za M a M za J (I < L < M < J), atd.Předpokládejme například, že cestujeme ze státu 1 do státu 3 a měny států 1, 2 a 3 se jmenují vony, tugriky a dongy. Jestliže za 1 von dostaneme 1,50 tugriku nebo 1,25 dongu a za 1 tugrik dostaneme 0,90 dongu, je výhodnější vyměnit vony nejdříve za tugriky a potom takto získané tugriky za dongy (za sto vonů tak dostaneme 135 dongů namísto 125 dongů, které bychom obdrželi přímou výměnou).
Napište a odlaďte program, který po načtení tabulky výměnných kurzů K dokáže odpovídat na otázky typu "jaký je nejvýhodnější (přímý nebo nepřímý) výměnný kurz při cestě ze státu I do státu J".
Vstupem programu (v souboru P-I-3.INP) je:
- kladné celé číslo N menší než 100 - počet států
- posloupnost N(N-1)/2 kladných reálných čísel - výměnné kurzy v pořadí K[1,2], K[1,3],..., K[1,n], K[2,3], K[2,4],..., K[2,n], K[3,4],..., K[n-2,n-1], K[n-2,n], K[n-1, n]
- kladné celé číslo P - počet vstupních dvojic ("otázek"), které budou následovat
- P dvojic celých čísel I, J (1 <= I < J <= N) - počáteční a koncové státy jednotlivých cest
P-I-3.OUT) bude P kladných
reálných čísel, která představují nejvýhodnější výměnné kurzy pro
jednotlivé cesty. Reálná čísla vypisujte s přesností na dvě
desetinná místa.
Příklad vstupu a odpovídajícího výstupu
P-I-3.INP
P-I-3.OUT
P-I-4
Kombinační obvod se skládá ze vstupů obvodu (označené I1, I2,...,In), z hradel (označené H1,H2,...,Hk) a z výstupů obvodu (označené O1,O2,...,Om). Každé hradlo má jeden nebo dva vstupy označené x (příp. y) a jeden výstup označený z. Každý vstup hradla Hi je napojen buď na některý vstup obvodu nebo na výstup některého jiného hradla Hj, j < i. Každý výstup obvodu Oi je napojen na výstup některého hradla.Vstupy a výstupy celého obvodu, stejně jako vstupy a výstupy jednotlivých hradel, se mohou nacházet v jednom ze dvou logických stavů 0 (false) nebo 1 (true). Výpočet obvodu je taktován. Jestliže jsou vstupy hradla H v čase t v logických stavech x[t] (příp. y[t]), výstup hradla H bude v čase t+1 v logickém stavu z[t+1] určeném vstupy a typem hradla. Pokud je na tento výstup napojen například vstup x' hradla H', bude v čase t+1 vstup x' v logickém stavu z[t+1], tzn. logický stav se po spojnicích šíří bez zdržení.
Budeme používat tři typy hradel: NAND, NOR (se dvěma vstupy)
a NOT (s jedním vstupem). Závislost výstupu těchto tří typů
hradel na vstupech je popsána následující tabulkou:
NAND
| x[t] | y[t] | z[t+1] |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR
| x[t] | y[t] | z[t+1] |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
NOT
| x[t] | z[t+1] |
| 0 | 1 |
| 1 | 0 |
Vstupem celého obvodu je n-tice logických stavů, v nichž se nacházejí jednotlivé vstupní body obvodu I1, I2,...,In. Logický stav vstupů obvodu se během výpočtu nemění. Hradla postupně reagují na logické stavy svých vstupů a mění podle toho stavy svých výstupů. Samozřejmě, jakmile se v čase t ustálí (tj. dále se nemění) logické stavy vstupů hradla, od okamžiku t+1 se ustálí také jeho výstup. Po konečném čase se ustálí i logické stavy výstupů obvodu. Výsledkem výpočtu je m-tice logických stavů jednotlivých výstupů obvodu O1, O2, ..., Om.
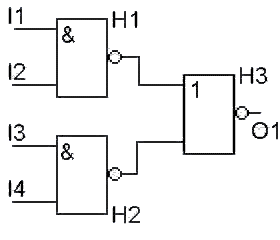
Obr. 1.
Například v případě obvodu na obr. 1 (hradla H1, H2 typu NAND se označují znakem &, hradlo H3 typu NOR označujeme symbolem 1) předpokládejme, že logické stavy vstupů obvodu jsou po řadě 0, 1, 1, 1. Od okamžiku t=1 bude logický stav výstupu hradla H1 roven 1 a logický stav výstupu H2 roven 0. Od okamžiku t=2 bude logický stav výstupu hradla H3 roven 0, což je také výsledek výpočtu.
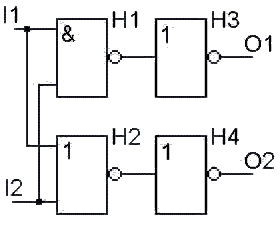
Obr. 2.
V obvodu na obr. 2 se objevují také hradla H3, H4 typu NOT (jsou označeny znakem 1, stejně jako hradla NOR, mají však pouze jeden vstup). Po dvou taktech (v čase t=2) se výstupy obvodu ustálí a výsledkem výpočtu bude "utříděný vstup": na výstupu O1 bude menší a na O2 větší z logických stavů na vstupech obvodu. Chování tohoto obvodu bychom mohli popsat tabulkou:| I1 | I2 | O1 | O2 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Úlohy
- Napište program, který ze vstupního souboru přečte postupně:
- tři čísla: počet vstupů obvodu (n), počet hradel (k) a počet výstupů obvodu (m)
- popis kombinačního obvodu ve vhodném formátu, který sami navrhnete
- číslo P: počet vstupních n-tic nul a jedniček
- P n-tic nul a jedniček: jednotlivé vstupy kombinačního obvodu
- Navrhněte kombinační obvod se dvěma vstupy (I1=x, I2=y) a dvěma výstupy (O1=c, O2=s) tak, aby realizoval sčítání dvou jednobitových čísel: 2c + s = x + y. To znamená, že výstup s bude obsahovat paritu součtu a výstup c bude obsahovat přenos (carry). Obvod nakreslete a popište ho i ve vstupním formátu pro váš program.