Matematická olympiáda – kategorie P

Řešení úloh ústředního kola (2. soutěžní den) 55. ročníku

P-III-4 Násobek

Označme si C množinu povolených číslic a N zadané číslo. Naší úlohou je najít nejmenší kladný násobek čísla N, ve kterém jsou použité jen číslice z C.

Zamysleme se nejprve nad jednodušší úlohou – jak zjistit, zda má zadaná úloha vůbec řešení?

Buď P množina všech kladných čísel, která se dají poskládat z cifer v C. Zjistíme, jaké zbytky dávají čísla z P při dělení N. Pokud bude mezi těmito zbytky i nula, úloha má řešení, pokud nebude, řešení nemá (žádný násobek N nemá požadovaný tvar).

Všimněme si jednoho zajímavého způsobu, jak můžeme definovat naši množinu přípustných čísel P:

Jednociferná přípustná čísla jsou právě všechny nenulové číslice z C.
Pokud je p∈ P a c∈ C, tak 10p+c∈ P.
Žádná jiná čísla v P nejsou.

Jinými slovy, všechna k-ciferná přípustná čísla umíme vygenerovat tak, že vezmeme všechna (k-1)-ciferná přípustná čísla a na konec jim připíšeme ještě jednu povolenou číslici.

Všimněme si teď, co se stane, máme-li dvě přípustná čísla p₁,p₂∈ P, která dávají po dělení N stejný zbytek z. Pokud za každé z nich připíšeme číslici c, dostaneme dvě nová přípustná čísla a opět obě budou dávat stejný zbytek po dělení N. (Tento zbytek bude (10z+c) mod N.)

Nyní už máme dost informací na to, abychom dovedli najít množinu Z zbytků, které dávají čísla z P po dělení N. Budeme výše uvedeným způsobem postupně generovat čísla z P. Vždy, když nějaké vygenerujeme, podíváme se, zda jsme dostali nový zbytek. Pokud ano, číslo si uchováme na další zpracování, pokud ne, zahodíme ho. (Všechny zbytky, které umíme vyrobit z tohoto čísla, umíme vyrobit i z toho, které dalo tento zbytek jako první.) Jelikož zbytků je jen konečně mnoho, jednou skončíme.

V tomto okamžiku už umíme rozhodnout, zda pro daný vstup existuje řešení. Po chvíli přemýšlení přijdeme i na to, že pokud jsme čísla z P generovali v rostoucím pořadí, tak v okamžiku, kdy jsme dosáhli zbytku 0, jsme ho dosáhli nejmenším možným číslem.

Pro zkušenější řešitele dodáváme, že výše uvedený postup odpovídá prohledávání do šířky v grafu, jehož vrcholy jsou zbytky po dělení N a každá hrana odpovídá přidání číslice, kteroužto číslicí si ji také označíme. V tomto grafu nyní najdeme nejkratší cestu z některého vrcholu odpovídajícímu jednocifernému číslu do vrcholu 0. Hrany vycházející z vrcholu vždy zpracováváme v rostoucím pořadí podle přidávané číslice. Hledané číslo může být velmi dlouhé, proto si pro každý zbytek pamatujeme jen to, ze kterého zbytku a přidáním které číslice jsme ho poprvé vytvořili. Pokud se nám podaří vytvořit zbytek 0, z těchto informací zpětně sestrojíme hledané číslo.

Časová i paměťová složitost tohoto řešení je O(N).

P-III-5 Stránka

Máme před sebou vlastně dvě samostatné úlohy. Tou první je porovnávání slov na stránce s vyhledávanými slovy. Potřebujeme co nejrychleji zjišťovat, kde se na stránce které vyhledávané slovo nachází.

Očíslujme si vyhledávaná slova od 1 do N. Text stránky převedeme na posloupnost čísel: místo vyhledávaného slova napíšeme jeho číslo, místo slova, které nás nezajímá, napíšeme nulu. (Pro příklad ze zadání dostaneme posloupnost 0, 0, 1, 0, 0, 0, 3, 2, 0, 0, 0, 0, 2, 0, 0, 0, 0, 1, 0, 0.)

Úseky stránky, které obsahují všechna vyhledávaná slova, nazveme dobré. (Každý dobrý úsek odpovídá v naší posloupnosti úseku, který aspoň jednou obsahuje každé z čísel 1 až N.)

Dobrý úsek, který už nemůžeme ani na jednom konci zkrátit, budeme nazývat minimální. Námi hledaný úsek je určitě minimální. Minimálních úseků ale může být i víc a všechny nemusí být stejně dlouhé. V našem příkladu jeden minimální úsek tvoří slova 3 až 8, druhý tvoří slova 7 až 18.

Naše řešení najde všechny minimální úseky a vybere z nich ten nejkratší.

Jak na to? Postupně pro každé slovo textu stránky zjistíme, zda tam začíná nějaký minimální úsek, a pokud ano, kde končí. Nahlédněme, že pro každé dva minimální úseky platí, že ten, který později začíná, také později končí. Proto když posouváme doprava začátek hledaného minimálního úseku, bude se i jeho konec posouvat jen doprava.

Abychom uměli rychle určit, zda je právě zkoumaný úsek dobrý, budeme si pamatovat následující informace: pocet[i] bude říkat, kolikrát se vyhledávané slovo i nachází ve zkoumaném úseku. Mimo to, mame bude počet vyhledávaných slov, která se vyskytují v aktuálním úseku aspoň jednou.

Když teď posuneme některý konec zkoumaného úseku o jedno slovo, změní se nám nejvýše jedna hodnota pocet[i] a na základě toho se případně (pokud jsme právě vynechali poslední výskyt některého slova nebo přidali slovo, které ještě v úseku nebylo) změní hodnota mame o 1.

Tím už máme tuto část úlohy vyřešenu. Začneme s úsekem, který tvoří jen první slovo textu stránky. V každém kroku se pak podíváme, zda je aktuální úsek dobrý. Pokud ano, vynecháme z něj jeho první slovo, pokud ne, přidáme k němu následující slovo textu.

V programu to může vypadat následovně:

{void nejkratsi_usek(int cisla[], int delky[], int *zacatek, int *konec)

  int nejlepsi = 987654321;
  int pocet[N+1] = { 0, };
  int mame = 0;
  int z = 0, k = 0, delka = -1;

  *zacatek = 0, *konec = 0;
  for (;;) {
    if (mame == N) {
      if (z == M)
        break;
      delka -= delky[z] + 1;
      pocet[cisla[z]]–;
      if (cisla[z] && pocet[cisla[z]] == 0)
        mame–;
      z++;
    } else {
      if (k == M)
        break;
      delka += delky[k] + 1;
      pocet[cisla[k]]++;
      if (cisla[k] && pocet[cisla[k]] == 1)
        mame++;
      k++;
    }
    if (mame == N && delka < nejlepsi)
      *zacatek = z, *konec = k, nejlepsi = delka;
  }
}

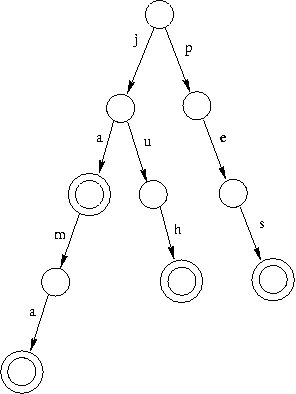
Písmenkový strom pro slova ja, jama, juh, pes.

Nyní se vraťme k první části úlohy: Jak efektivně přepsat slova textu stránky na čísla?

Jedno možné efektivní řešení je použít datovou strukturu zvanou písmenkový strom (anglicky trie). To je zakořeněný strom, ve kterém každý vrchol má nejvýše 26 synů a hrany do synů jsou označeny různými písmenky (od a do z). Každá cesta z kořene dolů odpovídá slovu, které si „přečteme” na hranách, po kterých jdeme.

Písmenkový strom se dá použít k uložení množiny slov: Vytvoříme všechny vrcholy, které jsou třeba na to, abychom si mohli „přečíst” každé z našich slov, a následně označíme ty vrcholy, v nichž některé ze slov končí. Například si k vrcholu můžeme poznamenat číslo dotyčného slova.

K vyřešení naší úlohy nám tedy stačí vytvořit písmenkový strom pro hledaná slova. Nyní pro každé slovo na stránce snadno zjistíme, zda je ve stromě uložené, a pokud ano, rovnou se dozvíme i jeho číslo.

Hledání slov má časovou složitost O(l_V + l_S), kde l_V je součet délek všech vyhledávaných slov a l_S součet délek slov tvořících text stránky (při stavění stromu i při vyhledávání spotřebujeme konstantní čas na zpracování každého písmene). Vyhledání minimálních úseků trvá O(N+M), ale jelikož N≤ l_V a M≤ l_S, můžeme celkovou časovou složitost odhadnout také výrazem O(l_V + l_S). Pokud si označíme délku nejdelšího slova L, lze totéž vyjádřit jako O((N+M)·L). Paměťová složitost je rovna časové.

Jiná možnost je použit místo písmenkového stromu hashování. Tehdy dosáhneme v průměrném případě asymptoticky stejné časové složitosti a pro velké slovníky i lepších multiplikativních konstant „schovaných do O-čka”.